MCMC (using emcee package)

Useful Functions

pyndamics3 version 0.0.32

source

dicttable

 dicttable (D)

source

time2str

 time2str (tm)

source

timeit

 timeit (reset=False)

source

corner

 corner (samples, labels)

source

histogram

 histogram (y, bins=50, plot=True)

Distributions – Defined for Speed

source

loglognormalpdf

 loglognormalpdf (x, mn, sig)

source

logbetapdf

 logbetapdf (theta, h, N)

source

lognormalpdf

 lognormalpdf (x, mn, sig, all_positive=False)

source

loghalfnormalpdf

 loghalfnormalpdf (x, sig)

source

loghalfcauchypdf

 loghalfcauchypdf (x, x0, scale)

source

logcauchypdf

 logcauchypdf (x, x0, scale)

source

logexponpdf

 logexponpdf (x, _lambda)

source

logjeffreyspdf

 logjeffreyspdf (x)

source

loguniformpdf

 loguniformpdf (x, mn, mx)

source

lognchoosek

 lognchoosek (N, k)

Distribution Classes

source

Beta

 Beta (h=100, N=100)

Initialize self. See help(type(self)) for accurate signature.

source

Cauchy

 Cauchy (x0=0, scale=1)

Initialize self. See help(type(self)) for accurate signature.

source

LogNormal

 LogNormal (mean=0, std=1)

Initialize self. See help(type(self)) for accurate signature.

source

HalfNormal

 HalfNormal (sigma=1)

Initialize self. See help(type(self)) for accurate signature.

source

HalfCauchy

 HalfCauchy (x0=0, scale=1)

Initialize self. See help(type(self)) for accurate signature.

source

Jeffreys

 Jeffreys ()

Initialize self. See help(type(self)) for accurate signature.

source

Uniform

 Uniform (min=0, max=1)

Initialize self. See help(type(self)) for accurate signature.

source

Exponential

 Exponential (_lambda=1)

Initialize self. See help(type(self)) for accurate signature.

source

Normal

 Normal (mean=0, std=1, all_positive=False)

Initialize self. See help(type(self)) for accurate signature.

Emcee functions

source

lnprior_function

 lnprior_function (model)

source

MCMCModel

 MCMCModel (sim, **kwargs)

Initialize self. See help(type(self)) for accurate signature.

source

MCMCModelReg

 MCMCModelReg (sim, verbose=True, **kwargs)

Initialize self. See help(type(self)) for accurate signature.

A linear growth example

Data from http://www.seattlecentral.edu/qelp/sets/009/009.html

from pyndamics3 import Simulation
t=np.array([7,14,21,28,35,42,49,56,63,70,77,84],float)
h=np.array([17.93,36.36,67.76,98.10,131,169.5,205.5,228.3,247.1,250.5,253.8,254.5])

py.plot(t,h,'-o')
py.xlabel('Days')
py.ylabel('Height [cm]')
Text(0, 0.5, 'Height [cm]')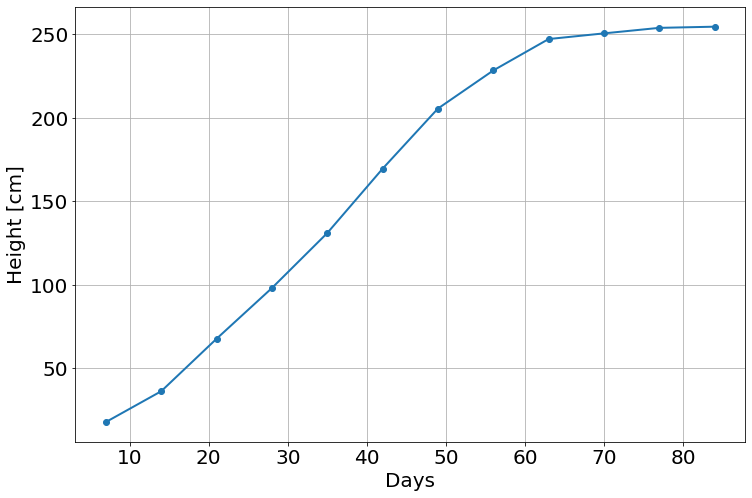

Run an initial (and bad) simulation

sim=Simulation()
sim.add("h'=a",1,plot=True)
sim.add_data(t=t,h=h,plot=True)
sim.params(a=1)
sim.run(0,90)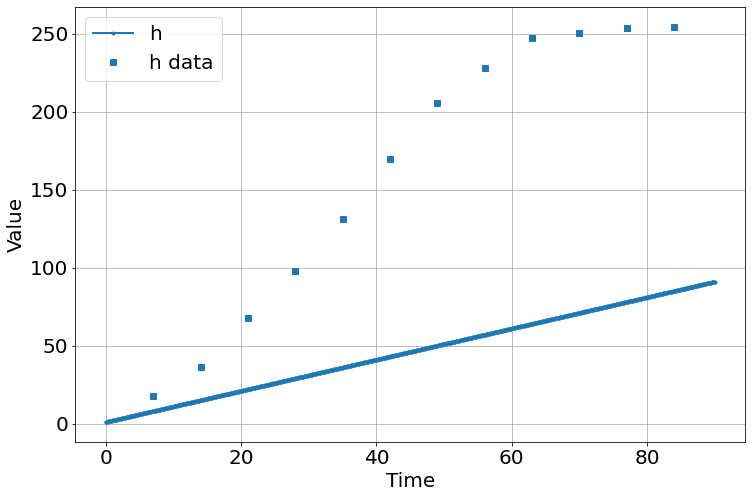

<Figure size 864x576 with 0 Axes>

Fitting \(a\)

model=MCMCModel(sim,a=Uniform(-10,10))

result=model.run_mcmc(500)
model.plot_chains()
Sampling Prior...
Done.
0.39 s
Running MCMC 1/1...
Done.
40.76 s
<Figure size 864x576 with 0 Axes>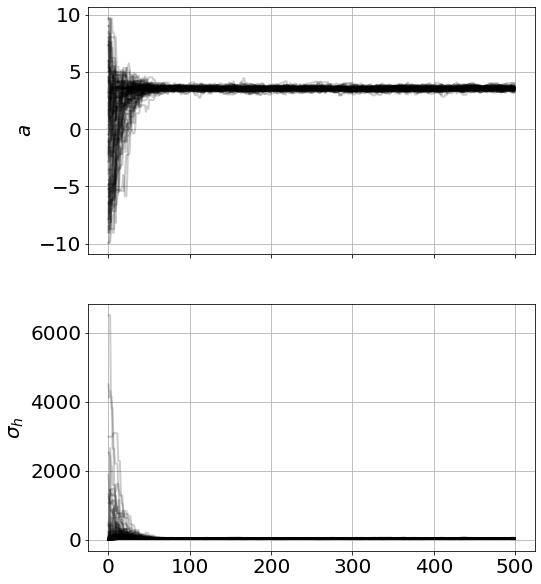

Although this looked converged, you might have situations where you want to repeat the mcmc-resample loop (i.e. resample parameters from the 95% CI of the current samples)

result

Priors

name

prior

a

Uniform
min -10
max 10

_sigma_h

Jeffreys

Fit Statistics

data points 12
variables 2
number of walkers 100
number of samples 37500
Bayesian info crit. (BIC) 112.50038192512125

Posteriors

name

value

2.5%

97.5%

a

3.5405

2.9562

3.825

_sigma_h

22.942

12.544

37.921

 
model.run_mcmc(100,repeat=3)
model.plot_chains()
Running MCMC 1/3...
Done.
8.47 s
Running MCMC 2/3...
Done.
8.21 s
Running MCMC 3/3...
Done.
8.20 s
<Figure size 864x576 with 0 Axes>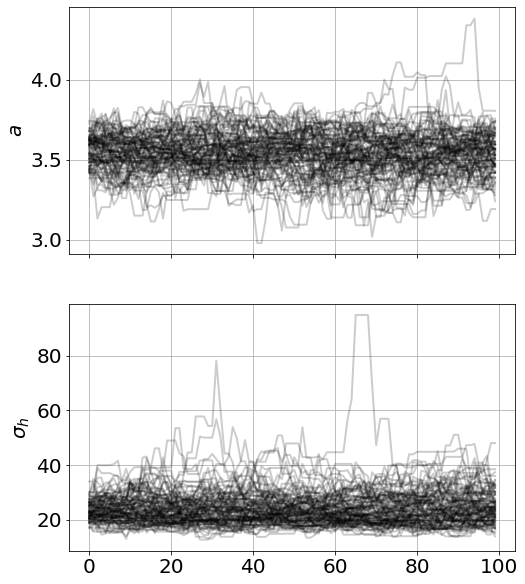

model.summary()

Priors

name

prior

a

Uniform
min -10
max 10

_sigma_h

Jeffreys

Fit Statistics

data points 12
variables 2
number of walkers 100
number of samples 7500
Bayesian info crit. (BIC) 112.50477437641784

Posteriors

name

value

2.5%

97.5%

a

3.5456

3.0126

3.7934

_sigma_h

22.97

12.659

39.585

 
model.best_estimates()
{'a': array([3.41276037, 3.5509136 , 3.6829332 ]),
 '_sigma_h': array([18.50769675, 22.69773539, 28.29713438])}
sim.run(0,90)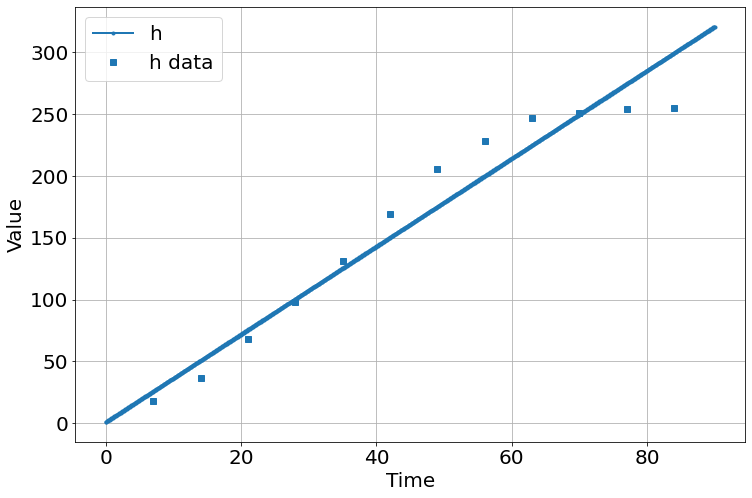

<Figure size 864x576 with 0 Axes>
model.plot_distributions()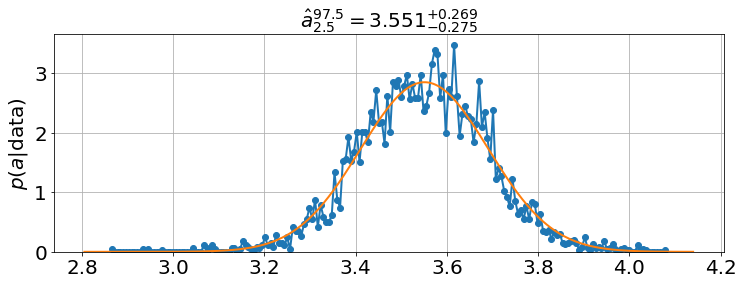

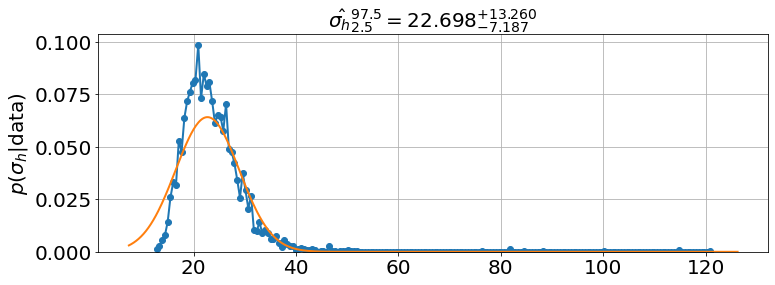
Fitting with \(a\) and the initial \(h\)

model=MCMCModel(sim,
                a=Uniform(-10,10),
                initial_h=Uniform(0,180),
                )
model.run_mcmc(500,repeat=2)
model.plot_chains()
Sampling Prior...
Done.
0.43 s
Running MCMC 1/2...
Done.
29.34 s
Running MCMC 2/2...
Done.
29.19 s
<Figure size 864x576 with 0 Axes>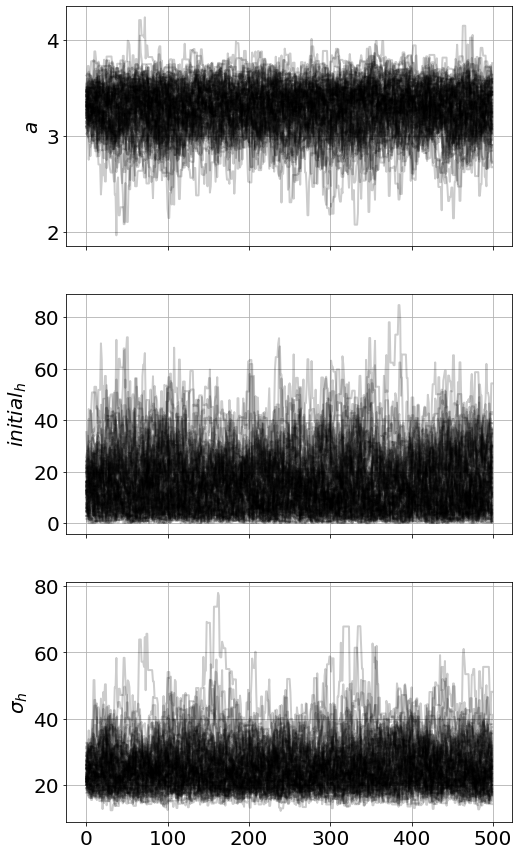

sim.run(0,90)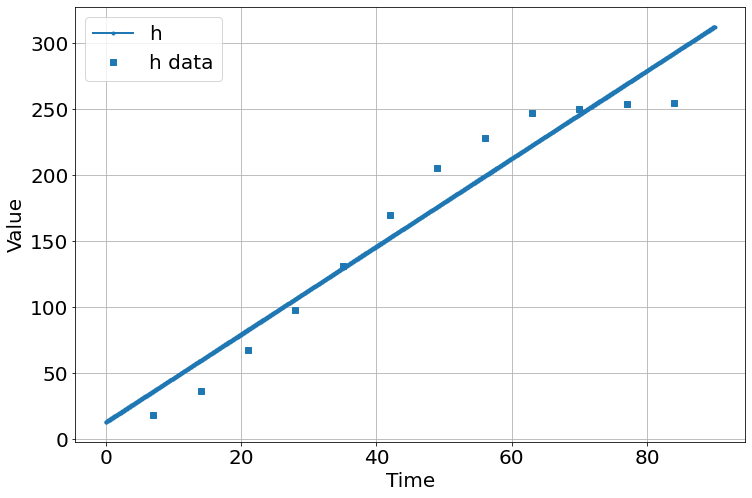

<Figure size 864x576 with 0 Axes>
model.plot_distributions()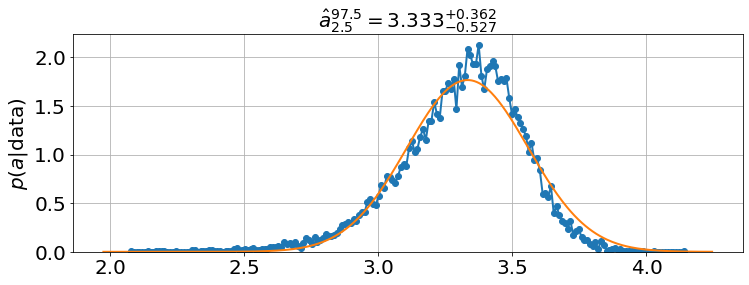

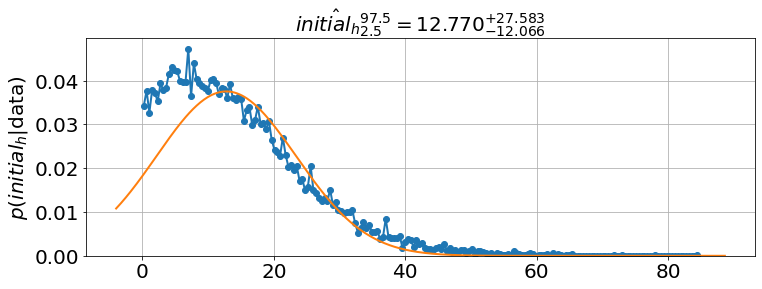
model.plot_many(0,90,'h')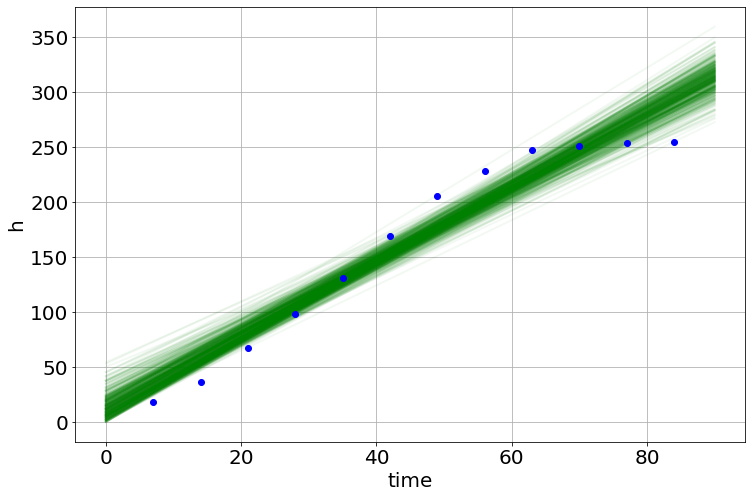

Logistic with the Same Data

t=np.array([7,14,21,28,35,42,49,56,63,70,77,84],float)
h=np.array([17.93,36.36,67.76,98.10,131,169.5,205.5,228.3,247.1,250.5,253.8,254.5])

sim=Simulation()
sim.add("h'=a*h*(1-h/K)",1,plot=True)
sim.add_data(t=t,h=h,plot=True)
sim.params(a=1,K=500)
sim.run(0,90)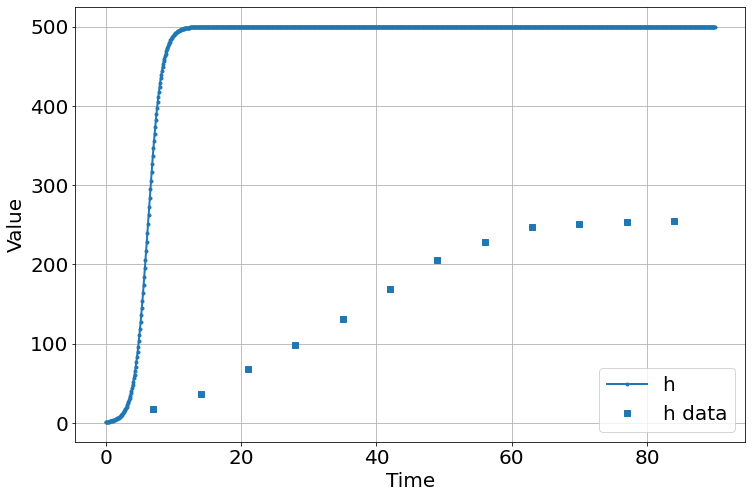

<Figure size 864x576 with 0 Axes>
model=MCMCModel(sim,
                a=Uniform(.001,5),
                K=Uniform(100,500),
                initial_h=Uniform(0,100),
                )
model.run_mcmc(500,repeat=3)
model.plot_chains()
Sampling Prior...
Done.
0.43 s
Running MCMC 1/3...
Done.
38.74 s
Running MCMC 2/3...
Done.
48.56 s
Running MCMC 3/3...
Done.
52.50 s
<Figure size 864x576 with 0 Axes>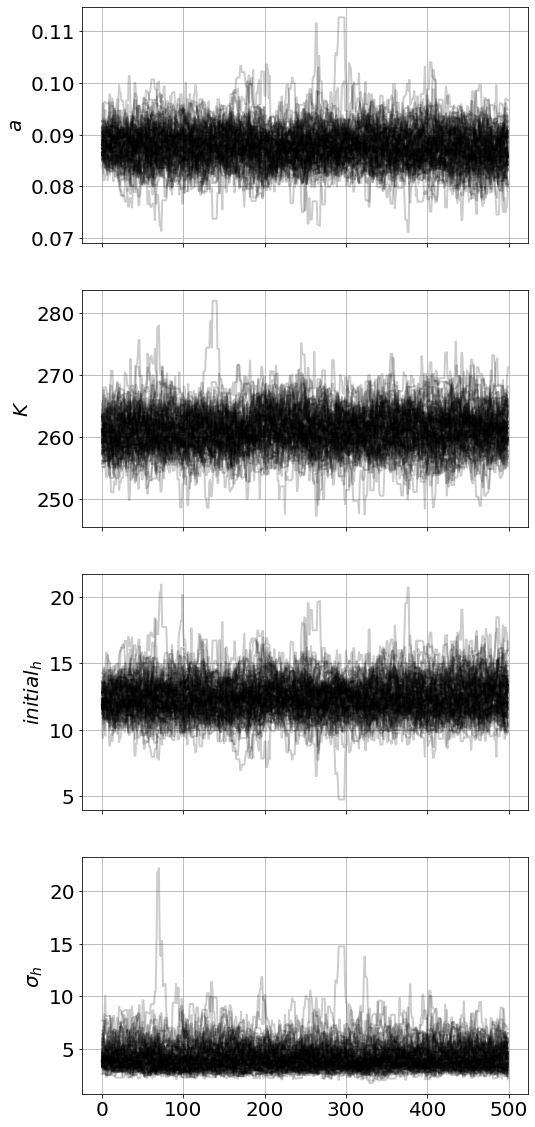

model.best_estimates()
{'a': array([0.08452244, 0.08754994, 0.09062923]),
 'K': array([258.46068768, 261.11871483, 263.83119905]),
 'initial_h': array([11.2367951 , 12.3431459 , 13.55099098]),
 '_sigma_h': array([3.12526592, 3.88416891, 5.06139448])}
sim.run(0,90)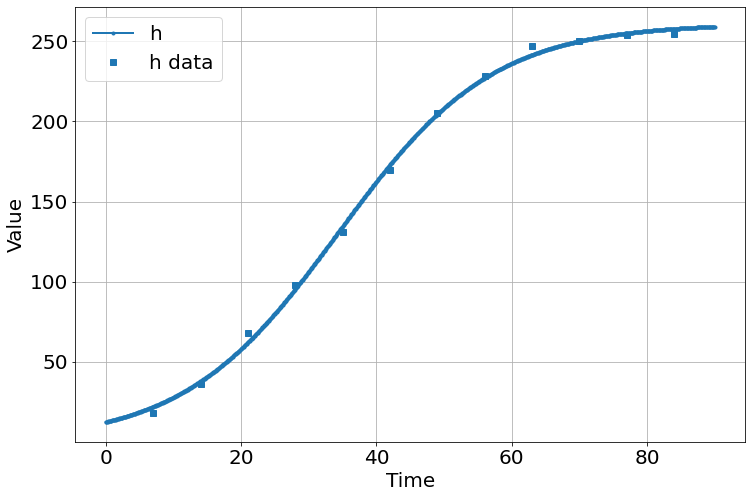

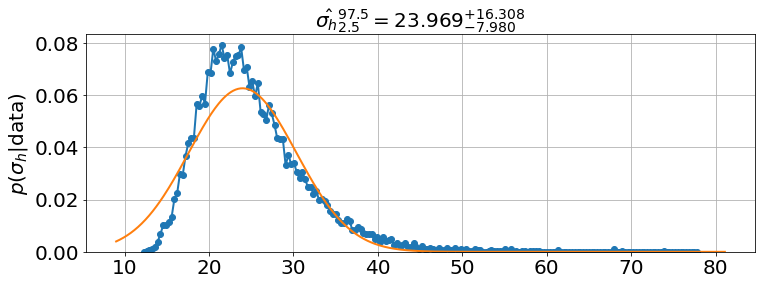
<Figure size 864x576 with 0 Axes>
model.plot_distributions()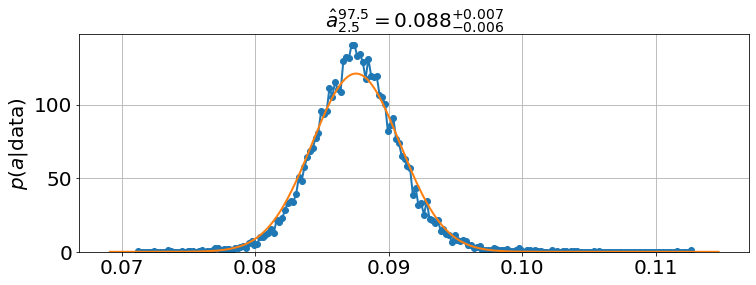

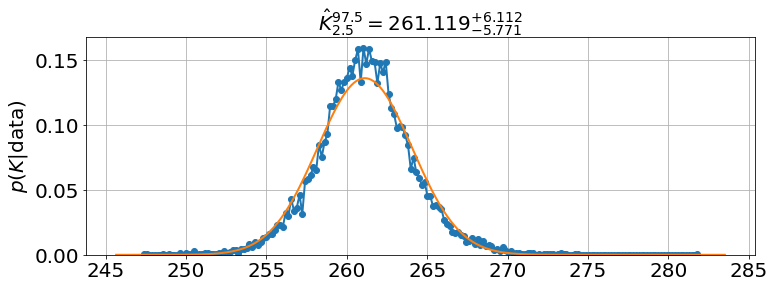
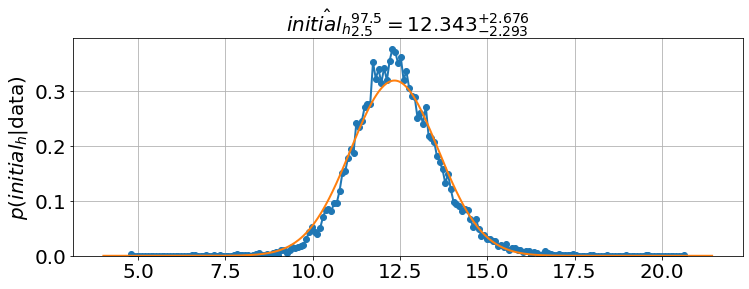
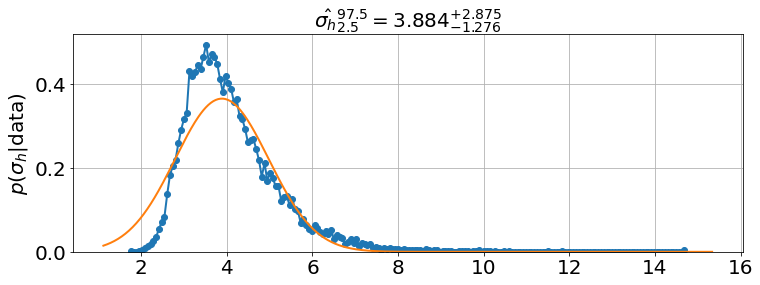
model.triangle_plot()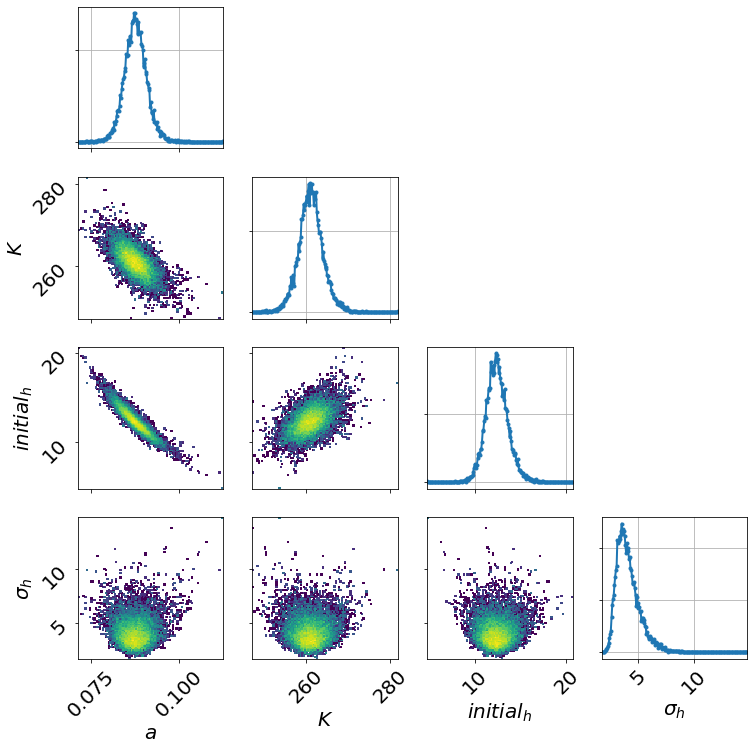

model.plot_many(0,90,'h')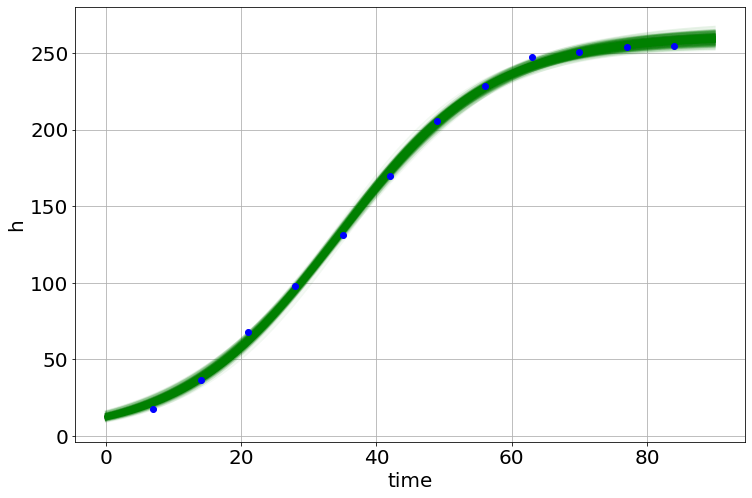

sim.noplots=True  # turn off the simulation plots
saved_h=[]
for i in range(500):
    model.draw()
    sim.run(0,150)
    py.plot(sim.t,sim.h,'g-',alpha=.05)
    saved_h.append(sim.h)
sim.noplots=False  # gotta love a double-negative
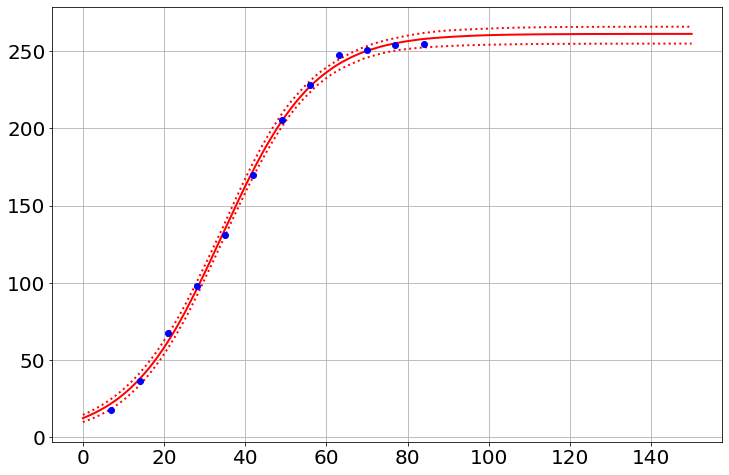
py.plot(t,h,'bo')  # plot the data
saved_h=np.array(saved_h)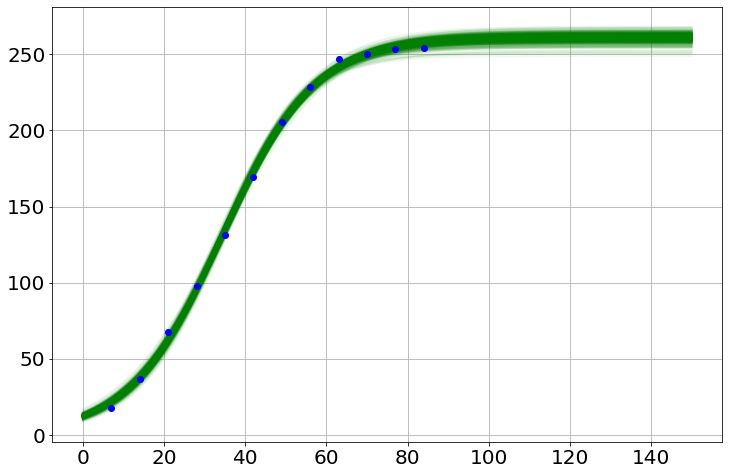

med=np.percentile(saved_h,50,axis=0)
lower=np.percentile(saved_h,2.5,axis=0)
upper=np.percentile(saved_h,97.5,axis=0)
py.plot(sim.t,med,'r-')
py.plot(sim.t,lower,'r:')
py.plot(sim.t,upper,'r:')

py.plot(t,h,'bo')  # plot the data