Statistics vs Probability

In #wordpress_migration

It's been a while since my last post, and I hope to get back into regularly posting, now that the semester is starting.  I'm also testing out new posting tools.

So, as a beginning, I start with an extract from an introductory statistics class:

I had a strong feeling that this was a job for probability, not for statistics, so I thought, how would one do this problem:

We observe  h1=4, N1=10

What is the probability of h2, N2=100?

It seems that the "probability" approach would be more fruitful, so I threw together this little calculation, where I simply marginalize over the single "random coin" parameter, given data 1 (our initial data) and look at the probability of various h2's:

1

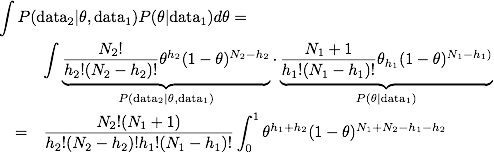
since

2

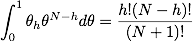
which also arises in the normalization condition for the beta distribution.  This leads to our final solution:

3

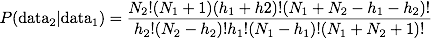
which leads to the following plot, for h1=4, N1=10, and N2=100:

4

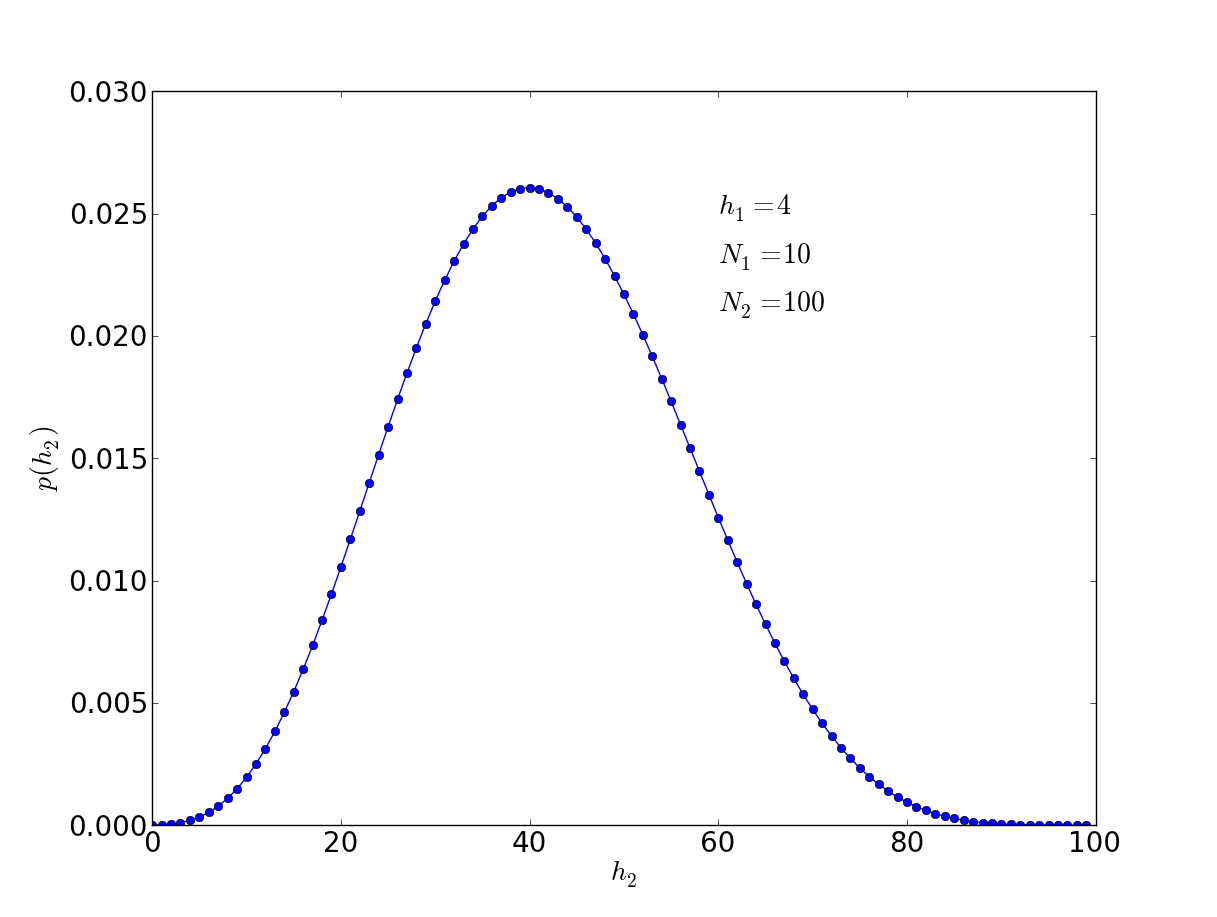
I can't help but think there is a simplification of the equation, but I don't see anything obvious that cancels.  Certainly, for large N's I could approximate it. 

Anyway, it is clearly a problem for probability not statistics...