Gravitational Attraction
What would happen if two people out in space a few meters apart, abandoned by their spacecraft, decided to wait until gravity pulled them together? My initial thought was that …
"Skeptics" vs "Realists"
A proposed solution
In #articles
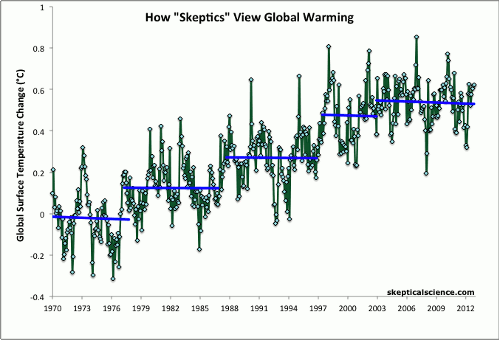
The graphic below has circulated the internet for a while, and I think it worthy of comment. The intent of the graphic is to point out how silly those so-called global warming "skeptics" are. However, I think there is a hidden proposal there as well, worthy of an undergraduate project.
If we call the "skeptics" model \(M_S\) and the "realists" model \(M_R\), then we want the following probabilities:
\begin{eqnarray}
P(M_S|{\rm data})
\end{eqnarray}
and
\begin{eqnarray}
P(M_R|{\rm data})
\end{eqnarray}
where the data is the temperature data for the past 40 years (or farther, if you want to compare to the entire known global temperature record).
The reason that we consider the "skeptics" model as potentially silly is the direct consequence of the probability analysis. The "realist" model has two parameters, so when we calculate the model probability we marginalize over those parameters.
\begin{eqnarray}
P(M_R|{\rm data})= \int_{\alpha,\beta} P(M_R|{\rm data},\alpha,\beta)P(\alpha,\beta)
\end{eqnarray}
where \(\alpha\) and \(\beta\) are the slope and intercept of the linear model, respectively. We incur an Ockham penalty for each marginalized parameter.
When we look at the "skeptics" model, we have the same.
\begin{eqnarray}
P(M_S|{\rm data})= \int_{\alpha_1,\beta_1,\alpha_2,\beta_2,\cdots,t_1,t_2,\cdots} P(M_S|{\rm data},\alpha_1,\beta_1,\alpha_2,\beta_2,\cdots,t_1,t_2,\cdots)P(\alpha_1,\beta_1,\alpha_2,\beta_2,\cdots,t_1,t_2,\cdots)
\end{eqnarray}
where \(\alpha_1\) and \(\beta_1\) are the slope and intercept, respectively, of the first line up to year \(t_1\). \(\alpha_2\) and \(\beta_2\) are the slope and intercept, respectively, of the second line up to year \(t_2\), etc.... Since we incur an Ockham penalty for each marginalized parameter, this model needs to fit the data substantially better than the "realist" model to achieve the same level of probability.
What does substantially mean? That is the proposal - perhaps someone will do this proper probabilistic analysis of the problem. Maybe the "skeptics" will turn out correct!
