Gravitational Attraction
What would happen if two people out in space a few meters apart, abandoned by their spacecraft, decided to wait until gravity pulled them together? My initial thought was that …
An Interesting Twist on the Gambler's Fallacy
In #math
I was reminded of the Gambler's Fallacy in a recent post by Stephen Novella and thought of a twist on the fallacy that makes it a bit more subtle. The fallacy is defined,
The gambler's fallacy, also known as the Monte Carlo fallacy or the fallacy of the maturity of chances, is the mistaken belief that, if something happens more frequently than normal during a given period, it will happen less frequently in the future (or vice versa). In situations where the outcome being observed is truly random and consists of independent trials of a random process, this belief is false.
If you observe 5 heads in a row, for example, then the probability of another heads is still \(p=0.5\). In other words it is not more (or less) likely to get a tails after a long string of heads in a row. There are however a couple of cases where this doesn't hold.
100 heads
What happens if you observe someone flipping a coin and they achieve 100 heads in a row. Would you really think that the probability of another heads is still \(p=0.5\)? Is it even rational to believe that? At some point, you would question the independence of trials assumption. You might think that the coin is rigged (two heads?) or that the flipping process is rigged (spinning the coin like a frisbee instead of end-over-end motion) or something else. The mathematics for it is pretty straightforward. Assume you have two models:
- \(M_1\): the coin-flipping process is random, trials are independent, and the probability of each flip is \(p=0.5\) for heads
- \(M_2\): the coin has two heads, so no matter what the flipping process is the probability of getting heads is \(p=1\).
and our data is \(m\) heads flips in a row
$$
D \equiv \left\{\underbrace{H_1,H_2,H_3,\cdots,H_m}_{\mbox{$m$ flips}}\right\}
$$
We are then interested in whether the \(m+1\) flip is a heads, or \(P(H_{m+1}|D)\). Since we have two possible models which could give this outcome, we break this probability into a sum for each,
$$
P(H_{m+1}|D) = P(H_{m+1}|D,M_1)P(M_1|D) + P(H_{m+1}|D,M_2)P(M_2|D)
$$
Since in both models the history of flips makes no difference to the next flip we get
\begin{eqnarray}
P(H_{m+1}|D,M_1) &=& P(H_{m+1}|M_1) = 0.5\\
P(H_{m+1}|D,M_2) &=& P(H_{m+1}|M_2) = 1
\end{eqnarray}
So, the bulk of the probability comes from the probability of each model given the data. Applying Bayes' Rule, we get
\begin{eqnarray}
P(M_1|D) &\sim& P(D|M_1)P(M_1)=\frac{0.5^m \cdot P(M_1)}{T} \\
P(M_2|D) &\sim& P(D|M_2)P(M_2)=\frac{1^m \cdot P(M_2)}{T}
\end{eqnarray}
where \(T\) is the total probability of the data and the probabilities \(P(M_1)\) and \(P(M_2)\) are the priors for Model 1 and Model 2, respectively.
We can start figuring out the prior probability by thinking in the following way. Since we usually don't think a system is rigged unless we start seeing a strong pattern consistent with that, we expect that the prior for \(M_2\) should be much less than for \(M_1\). Without loss of generality, we assign \(P(M_1) = 1\) and \(P(M_2) = 10^{-a}\). If \(a=3\) then Model 2 is 1000x less likely (before the data) than Model 1, if \(a=6\) then Model 2 is 1 million times less likely, etc... We consider that the coin might not be independent when the probabilities for the two models -- after the data -- become comparable. Each heads observation makes Model 1 a bit less likely and Model 2 a bit more so. In a picture (for the case of \(a=6\)) we have
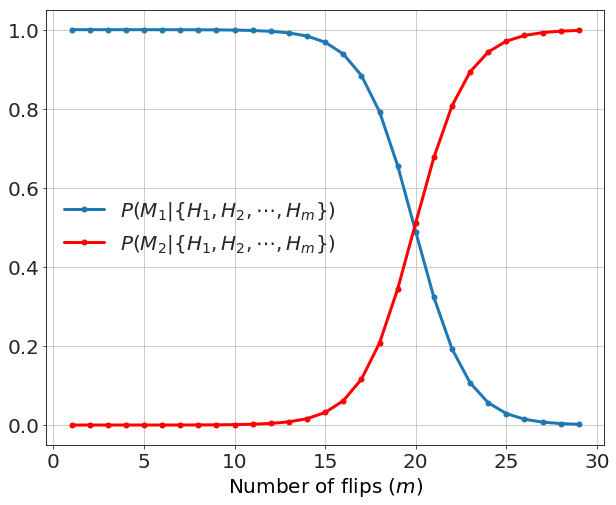
Mathematically we have
$$
\frac{P(M_2|D)}{P(M_1|D)} = \frac{10^{-a}}{0.5^m} \gt 1
$$
which yields the number of flips, \(m\), to overcome a prior against the two-headed coin, \(a\),
$$
m> \frac{a}{\log_{10} 2}
$$
For \(a=6\) (or initially a million times less likely) then \(m>19.9\) flips is needed to overcome that level of initial skepticism.
Alternating Results or Quasi-random processes
The same sort of analysis can occur if instead of a string of heads we observe a perfectly oscillating sequence (H,T,H,T,H,T,...). This, of course, could be the result of a random process but if it continued long enough then even a low prior of a rigged system could be overcome.
The same could occur if you happen to be observing a Sobol Sequence or some other quasi-random processes. These sequences are designed to be non-independent in order to be more likely to fill the space of numbers evenly. Thus, if there is a sequence of 5 heads in a row, then under a quasi-random process a tails is in fact more likely in these sequences as the "fallacy" warns us against. These processes have some use in sampling for simulations where you want to make sure to cover all the the values of the parameter space evenly and efficiently.
Conclusion
I am not arguing that the Gambler's Fallacy is wrong, nor am I arguing that we should think every case is rigged. I am further not suggesting that people are actually good at these problems - they aren't. We see patterns in random sequences and events all of the time, and perhaps we should be a bit more reticent to ascribe non-randomness to processes for which we have no evidence of a non-random influence. In other words, our priors for a rigged system should generally be quite low. However, there can be cases where the system is rigged and we should be open to that possibility as well.
