Stats 101 Examples with MCMC

Estimating mean with known 𝜎

In #math

I'd like to walk through some of the "Statistics 101" examples (e.g. estimating μ\mu with known σ\sigma, estimating a proportion, etc...) for which we have simple analytical solutions, but explore them with MCMC. The reason I want to do this is to introduce MCMC on simple cases, which are not much different than more complicated cases, but are better understood. The second reason is to explore some cases which are nearly as easy, but are never covered in introductory textbooks. In all of these I'm going to use a python library I make for my science-programming class, stored on github, and the emcee library. Install like:

pip install "git+https://github.com/bblais/sci378" --upgrade
pip install emcee

We'll start with the easiest example: there is some true value, we call μ\mu. The NN data points we have, {xi}\{x_i\}, consist of that true value with added independent, normally-distributed noise of known scale, σ\sigma.

For a Bayesian solution, we need to specify the likelihood function -- how our model produces the data -- and the prior probability for the parameters. The likelihood function is determined like

xi∼μ+ϵiP(xi∣μ,σ)∼Normal(xi−μ,σ)P({xi}∣μ,σ)∼∏iNormal(xi−μ,σ) \begin{aligned} x_i &\sim \mu + \epsilon_i \\ P(x_i|\mu,\sigma) &\sim \text{Normal}(x_i-\mu,\sigma) \\ P(\{x_i\}|\mu,\sigma) &\sim \prod_i \text{Normal}(x_i-\mu,\sigma) \end{aligned} known σ\sigma

In the "Statistics 101" examples, the results are typically equivalent to uniform priors on the parameters, so we'll assume uniform priors on μ\mu. 

def lnlike(data,μ):
    # known σ
    x=data
    return lognormalpdf(x,μ,σ)

data=array([12.0,14,16])
σ=1
model=MCMCModel(data,lnlike,
                μ=Uniform(-50,50),
                )

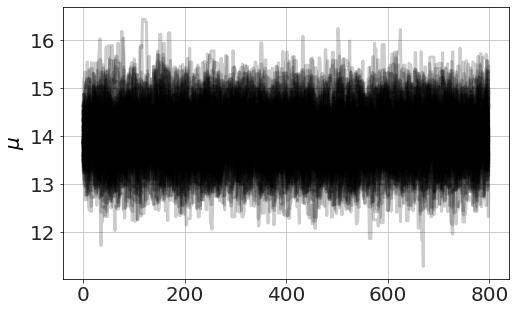
now we run MCMC, plot the chains (so we can see it has converged) and look at distributions,

model.run_mcmc(800,repeat=3)
model.plot_chains()

Sampling Prior...
Done.
0.21 s
Running MCMC 1/3...
Done.
2.23 s
Running MCMC 2/3...
Done.
2.24 s
Running MCMC 3/3...
Done.
2.51 s


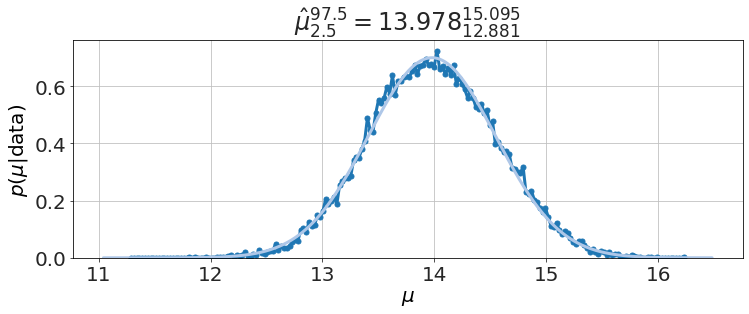
model.plot_distributions()

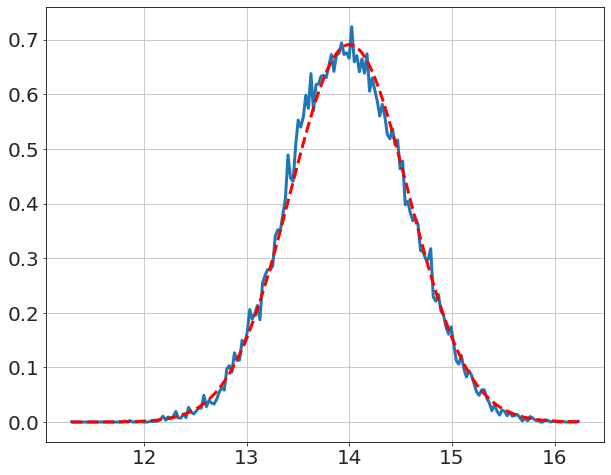
compare to textbook solution (i.e. Normal with deviation σ/N\sigma/\sqrt{N}),

x,y=model.get_distribution('μ')
plot(x,y,'-')
μ̂=mean(data)
N=len(data)
σμ=σ/sqrt(N)
y_pred=[exp(lognormalpdf(_,μ̂,σμ)) for _ in x]
plot(x,y_pred,'r--')

and finally find a tail-area probability, the Bayesian equivalent to Z-test,

model.P('μ>15')

0.037066666666666664

This simple example can be a template for more complex problems, which I will explore in later posts of this series. What do you think?