Fitting parameters in dynamics systems

using lmfit with pyndamics

In #programming

A while ago I wrote this little package called pyndamics which was a thin wrapper around the scipy odeint function. Since then I migrated it using nbdev to experiment with using jupyter notebooks as the basis for making packages, yielding pyndamics3. I added MCMC support for parameter fitting fairly early, using PyMC, but changed to emcee to have an all-python implementation. (This past month, after upgrading to Big Sur on my Mac, I've been struggling to even install PyMC3 and pystan due to dependencies but that is another story).

Recently, it struck me that the lmfit package might be a straightforward way to add some curve fitting that would work with simpler systems, and take less time than running MCMC. So, now pyndamics3 can use lmfit as a fitting backend. For example,

fitting linear growth

%pylab inline
from pyndamics3 import Simulation

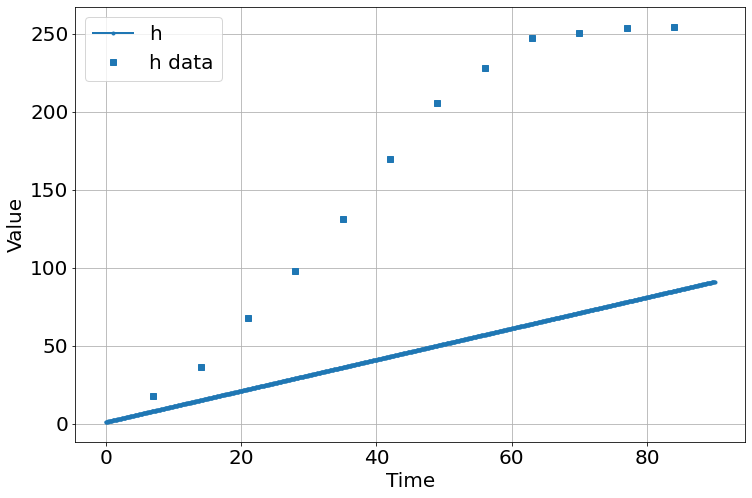
t=array([7,14,21,28,35,42,49,56,63,70,77,84],float)
h=array([17.93,36.36,67.76,98.10,131,169.5,205.5,228.3,247.1,250.5,253.8,254.5])

sim=Simulation()
sim.add("h'=a",1,plot=True)
sim.add_data(t=t,h=h,plot=True)
sim.params(a=1)
sim.run(0,90)


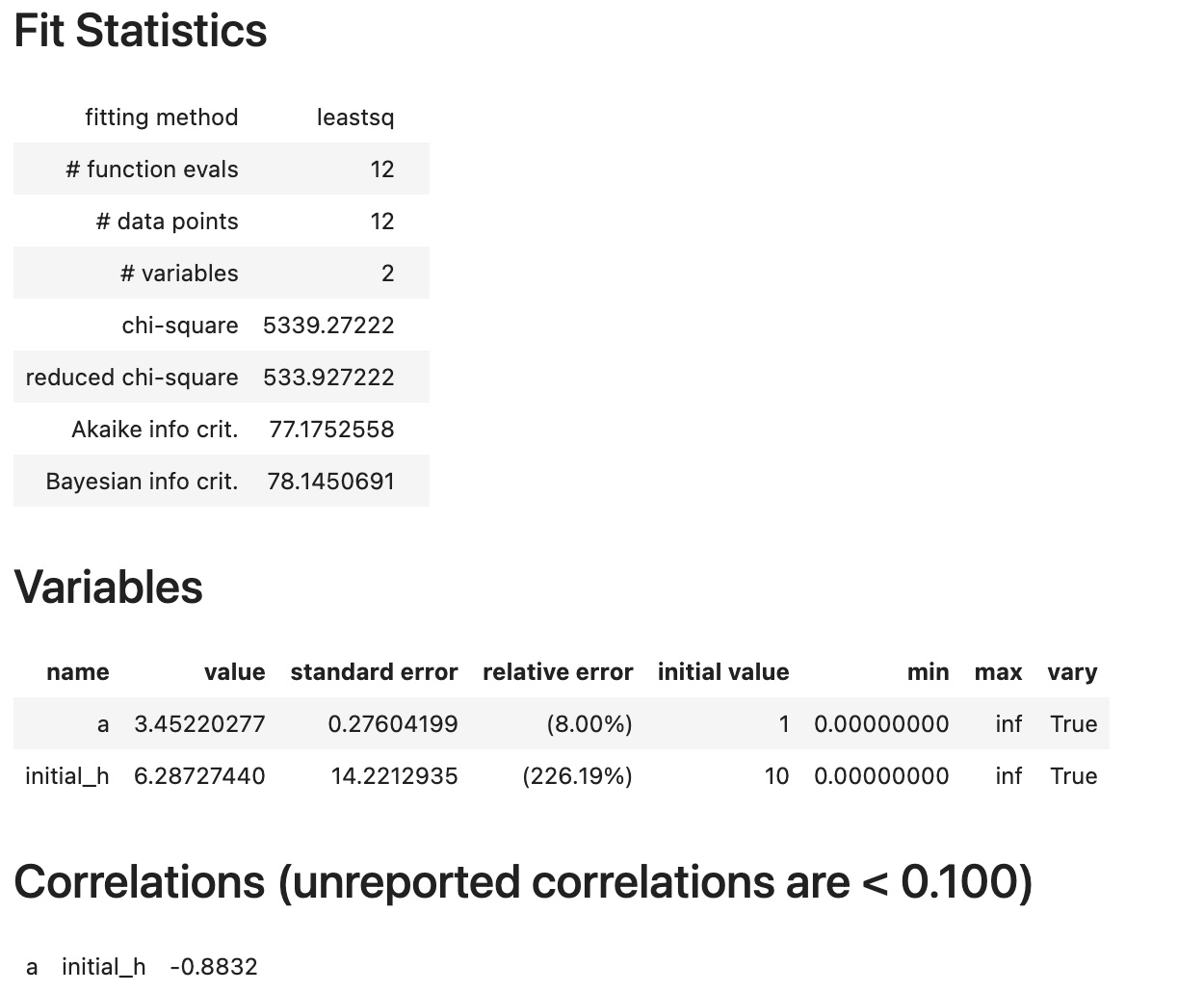
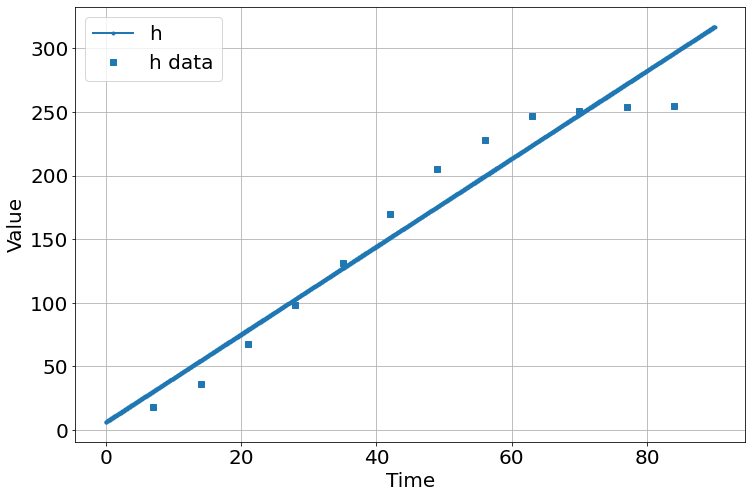
from pyndamics3.fit import fit,Parameter
results=fit(sim,
   Parameter('a',value=1,min=0),
   Parameter('initial_h',value=10,min=0))

results

Or with logistic growth

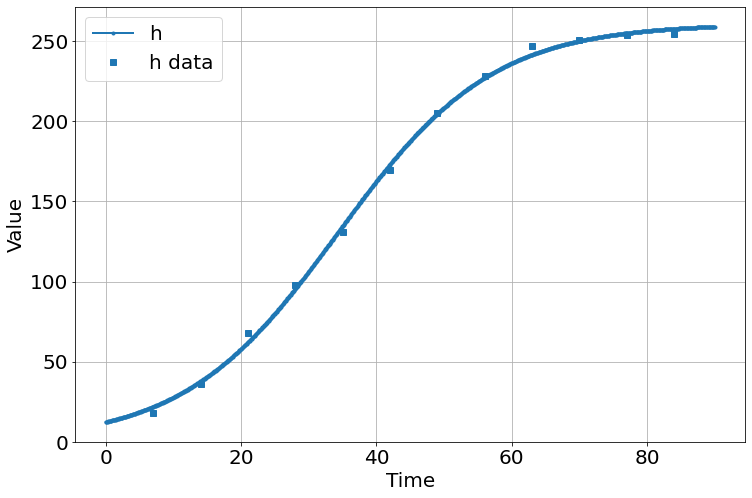
sim=Simulation()
sim.add("h'=a*h*(1-h/K)",1,plot=True)
sim.add_data(t=t,h=h,plot=True)
sim.params(a=2,K=100)
sim.run(0,90)

with 

results=fit(sim,
   Parameter('a',value=1,min=0.01,max=2),
   Parameter('K',value=1,min=0,max=400),
   Parameter('initial_h',value=10,min=0,max=50),method='powell')

report_fit(results)

sim.run(0,90)

(notice specifying the method).