Chemical Reaction Dynamics

Reproducing a Computational Paper

In #science

As an exercise, I like to reproduce computational papers, but with my own tools. This let's me know that I understand completely what is being written and in many cases allows me to extend and debug my own tools. I'm going to do a series of these as I work through some of my reading list. The first one I'm doing is available here:

https://www.cs.princeton.edu/picasso/mats/matlab/princeton_spring06.pdf

In this case, not only was I able to reproduce the results of the text, but it uncovered two bugs in my pyndamics3 package which I was able to fix.

The main system in the text being solved is

Pasted image 20220113102335.png

%pylab inline

from pyndamics3 import Simulation
from pyndamics3.chem import ChemSimulation

b=20
k3=0.00577
k4=0.0001925
k1=.01

sim=ChemSimulation(
"""
D --k1--> D+M
M --k2--> M+P
M --k3--> ϕ
P --k4--> ϕ
""",D=1,M=0,ϕ=0,P=0,k1=k1,k2=b*k3,k3=k3,k4=k4)

for c in sim.components:
    c.plot=True

sim.run(4e4)

Output:

['D'] k1 ['D', 'M']
['M'] k2 ['M', 'P']
['M'] k3 ['ϕ']
['P'] k4 ['ϕ']
Components ['D', 'M', 'P', 'ϕ']
Parameters ['k1', 'k2', 'k3', 'k4']
diffeqs ["D' = 0", "M' =  +k1*D -k3*M", "P' =  +k2*M -k4*P"]

which yields figures like:

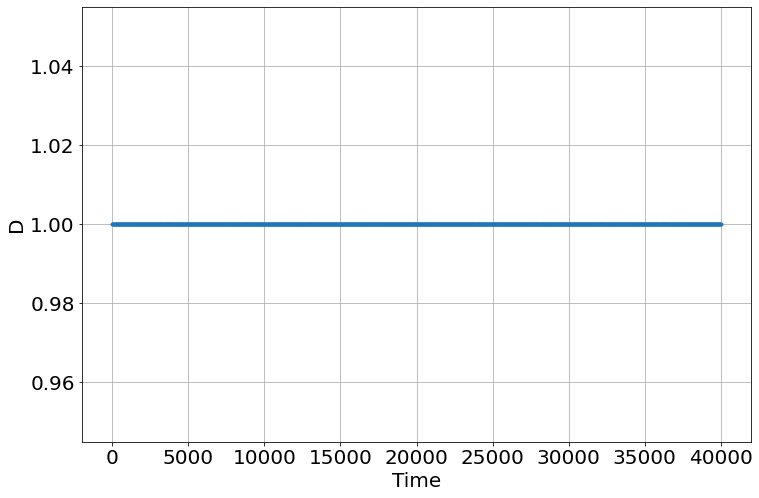
Pasted image 20220113102516.png

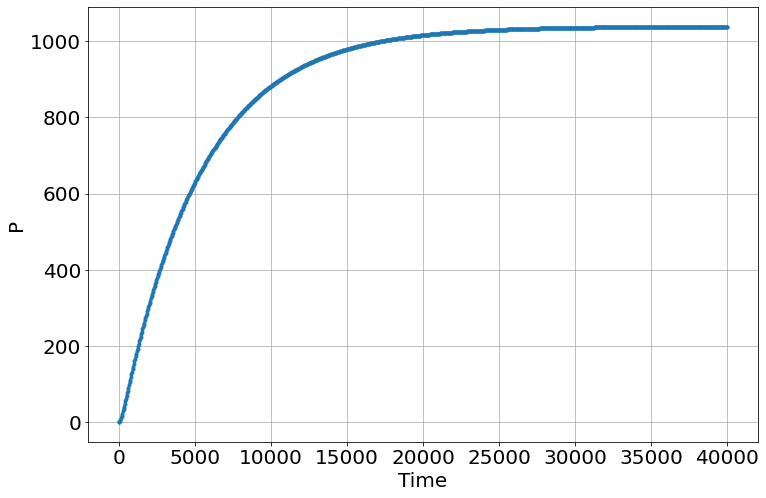
Pasted image 20220113102541.png Pasted image 20220113102550.png

The text points out,

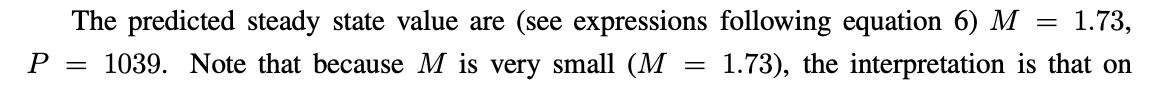
Pasted image 20220113102608.png

which we can find by looking at the end of the array for each of those variables.

sim.P[-1],sim.M[-1]

(1038.4743123361338, 1.7331022510164473)

The paper then adds the exercise

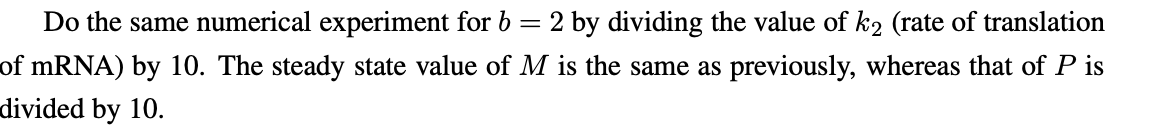
Pasted image 20220113102710.png

b=2
k3=0.00577
k4=0.0001925
k1=.01

sim=ChemSimulation(
"""
D --k1--> D+M
M --k2--> M+P
M --k3--> ϕ
P --k4--> ϕ
""",D=1,M=0,ϕ=0,P=0,k1=k1,k2=b*k3,k3=k3,k4=k4)


for c in sim.components:
    c.plot=True

I discovered that by originally doing

sim.run(1e4)

sim.P[-1],sim.M[-1] 

(88.21709421325941, 1.7331022259104094)

it didn't match the fixed point stated in the text! So Iooked at the plot

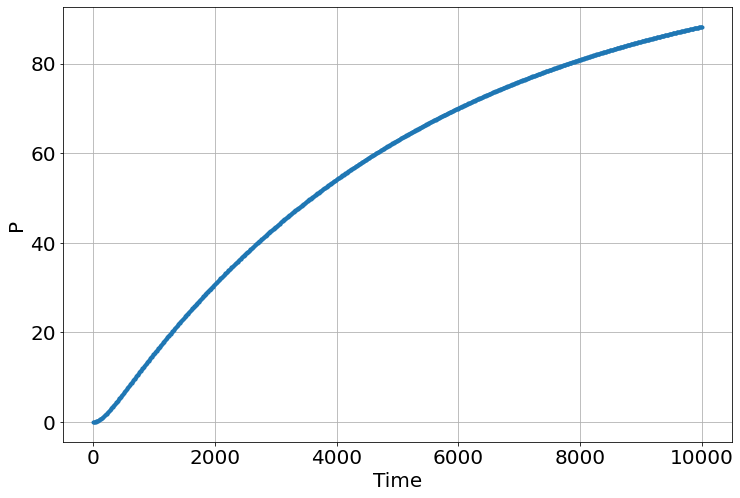
Pasted image 20220113103003.png

and saw it hadn't converged. Increasing the run time

sim.run(1e5)

sim.P[-1],sim.M[-1]

(103.8961031134814, 1.7331022530369293)

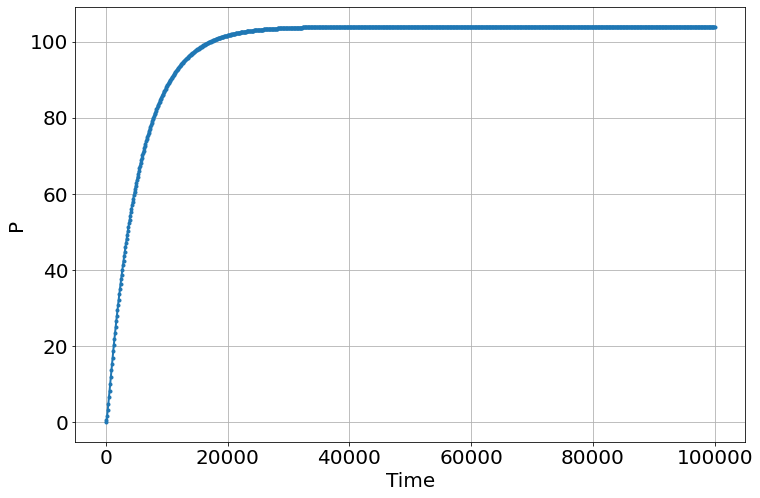
Pasted image 20220113103146.png

It converged and we got the same answer as in the text.

Another time I will extend this to the stochastic version, which is in the second part of the text.