The Nines Deck and Scientific Reasoning

I wrote about the Nines Deck here as an example of multiple model comparison. Here I want to extend the example to explore more about scientific reasoning.

I ended my post with the following:

The non-monotonic effect is also why, when a psychic demonstrates some amazing feat of apparent mind-reading, they still won't be believed immediately. This is because many rare and unconsidered explanations will rise from low prior status to dominate. These low prior models still have a higher prior value than the ESP model, but are low enough to not be considered immediately. The next step would be to modify the data collection process to potentially eliminate them. In other words, to design an experiment to rule out these alternate explanations. This is the process of science -- designing experiments to make these low prior models less likely in the hope of increasing the probability of the model under consideration.

I do find that proponents of pseudoscientific claims get frustrated with this process. They don't understand how, once the high-prior alternative explanations have been removed that their magical claim is not immediately believed. Instead, new models never discussed rise to the surface and have to be dealt with. Accusations of naturalistic or other bias against their claims come out, the investigator is accused of being "too skeptical", of never being convinced no matter what the evidence. This comes from a lack of understanding of how probability actually works, usually because the versions of these same calculations are done with binary models, lack of imagination, and no attempt at verifying the numbers.

So I have been trying to think of good analogies to the process of ruling out high-prior explanations which seem to point to extremely low-prior explanations, but along the way raising some somewhat low-prior explanations. Going back to my High-Low-Nines deck example, I'll draw out the analogy.

• The High and Low deck explanations are mundane
• The Nines deck is an extremely low-prior explanation -- like the ESP model, or the Resurrection model described by apologists.
• The string of $m$ 9's in a row is a string of data all consistent with the low-prior explanation.

The way that apologists would see it, we have a lot of data which is consistent with their explanation. They rule out some of the simple alternatives, which leaves their preferred explanation, so you should believe their explanation. That's like the figure in end of my post on the High-Low-Nines example.

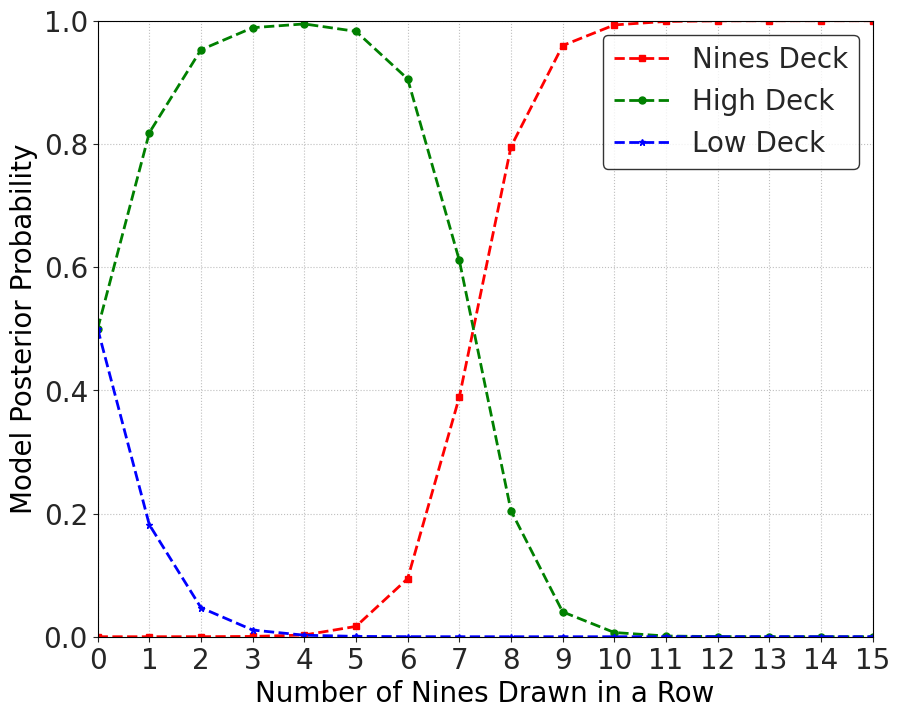
I want to comment that the typical formulation of Bayes theorem from the apologists is in the odds-form -- a ratio of the probabilities of two models, or rather, one model and it's negation. However, the result just shown and the entire discussion below is either impossible to see in the odds form or is much less clear. As such, the thinking of the apologist is restricted to binary comparisons and the complexity of actual rational inference is lost to them.

Now one might quibble about whether the apologist has the necessary amount of data to overcome the prior, but let's leave that for now. In my original post, after a long string of 9's one can posit a few explanations. There could be the very-rare Nines deck, or we could be looking at the High or Low deck still but that the shuffling wasn't done properly. It may have looked like the process shuffled, or we might not have seen it and were just told it was reshuffled. So another set of models could be an unshuffled Low deck or unshuffled High deck -- we keep taking the top card, which happens to be the same card every time. While this a more nuanced explanation it does not introduce another kind of deck. As such, it has a very low prior at the start but higher than the Nines deck explanation. What would this look like? In the following figure I am having the unshuffled versions of the Decks have a prior of 1/1000 -- still very small, but larger than the prior for the Nines.

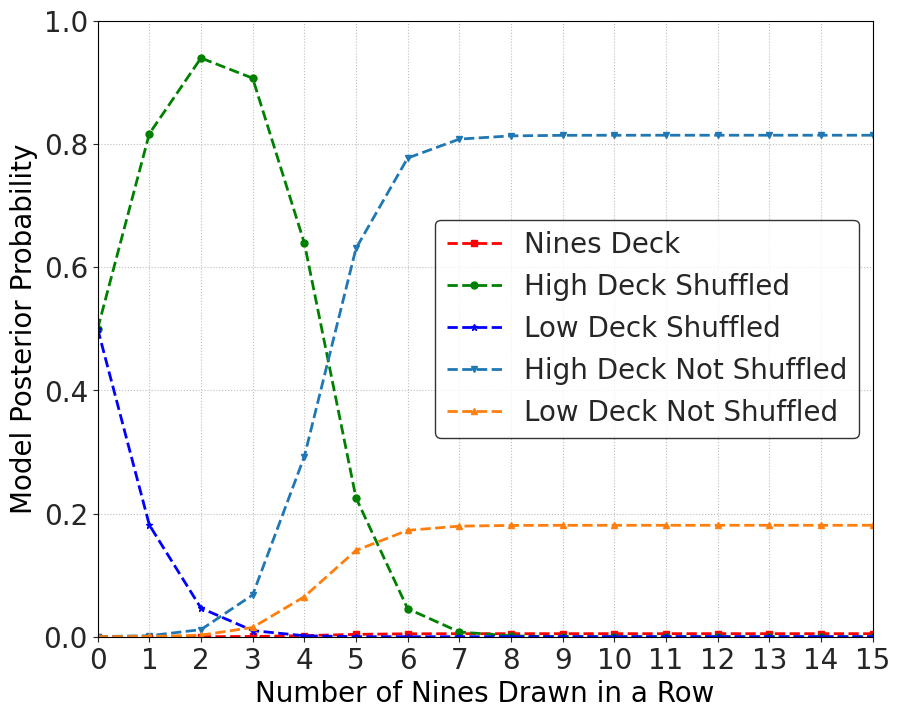
What we can see is that the continued stream of 9's is consistent with the more mundane unshuffled models and thus the rare Nines explanation never rises to believability -- and never will. Now the apologist-scientist seeing this, and trying to rescue the Nines model, would propose an experiment. After about 10 draws it's pretty clear nothing is happening, so the apologist-scientist decides to change the procedure a bit (i.e. the experiment). While not having access to the shuffling (or not) mechanism, the apologist-scientist decides to draw from the bottom rather than from the top. This at least makes the possibility of falsifying the Nines model, if anything other than a 9 appears. If a 9 appears, it should make the Nines model more likely and the other models should go down (at least that's the intuition). Here's the result:

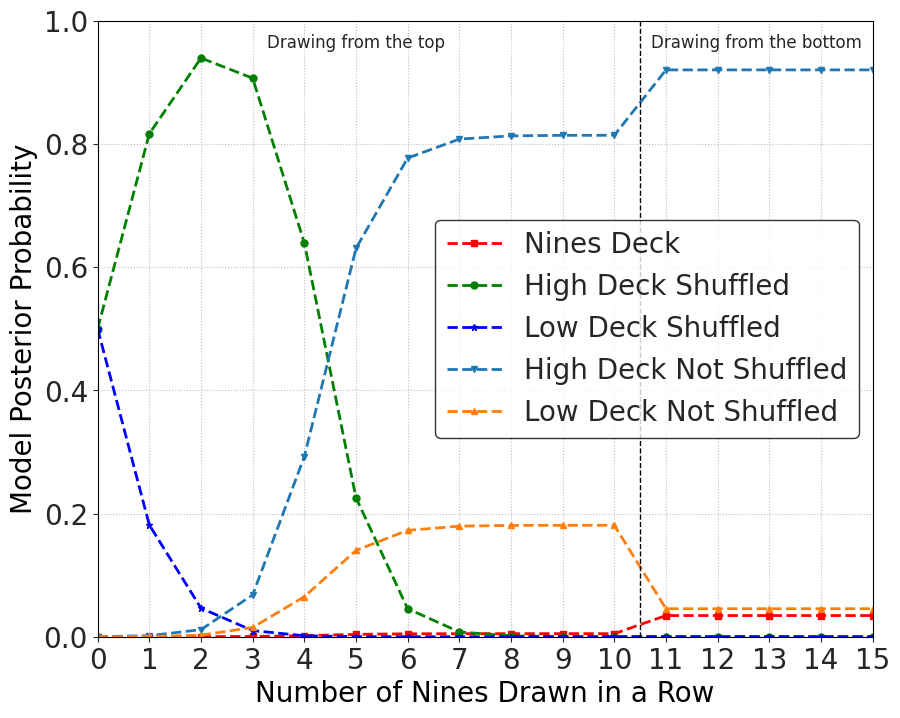
While drawing from the bottom and seeing another sequence of 9's does increase the probability of the Nines deck, the unshuffled High Deck probability goes up! Most of the loss of the unshuffled Low Deck probability gets reassigned to the unshuffled High Deck with only a modest increase in the Nines deck probability. This violates some of our intuition, but that is one of the values of doing the probability analysis -- it allows us to learn a more sophisticated intuition. Also, it should remind us that testing results, being quantitative, and having more than one way to look at a problem are all invaluable.

One might critique the scientist saying that, if you don't have access to the shuffling mechanism, then don't just draw from the bottom, draw from a random part of the deck. In some cases in science, there are some experiments we don't have access to, and can only do a limited number of types of measurements. In history, we don't have a time machine, and sometimes the data just isn't enough to answer certain questions. We just don't have access or control of the data to address them. That's why the conclusions in history are always much more uncertain and tentative than in the sciences.

As a reminder, none of these effects would be observable to the apologist who insists on writing the math in odds-form.

It is my hope that this simple example can structure a conversation around many topics, and get us away from simplistic Bayesian arguments that use the odds-form. I find that this toy model of the High-Low-Nines deck allows us to play with our intuitions, explore analogies in an example which has some nice parallels with scientific reasoning. Are there other ways of framing this analogy that are more clear and help with communication?

What problems are you interested in? How can I help?

• @bblais
• bblais@bryant.edu
• (401) 232-6153
• Bryant University
  1150 Douglas Pike
  Smithfield, RI
  02917 US