I read with interest this article by Than Christopoulos after seeing his debate with Matt Dilahunty which I hope to respond to at some point. Than is very excited about Bayes Theorem and he likes to apply it to religious contexts, both of which are interests of mine, so I got to nerd-out in his article for a while. I like the approach Than uses, and he goes out of his way to insert teaching examples to help the reader along which is nice, but I was disappointed with some of the statements Than made about Paulogia and his motives. Than says about Paulogia "Why offer detailed engagement with a nuanced model when you can say something that sounds smart—especially if you say it with confidence and derision? It’s a pattern I’ve encountered firsthand." One of the points I wish to make in this post is that much of the disagreement which sparked Than's blog post is that the two are talking about different things -- and I hope to show this using Bayesian analysis so that Than will more clearly understand. But to claim that Paulogia is just trying to take cheap shots and can't handle nuance is ridiculous. Just go and watch any of his videos (like Who REALLY wrote the Gospels and How NOT to Defend the Resurrection Against Minimal Witnesses) to see that Paulogia is one of the most careful and considered YouTubers in the field and that it is not a coicidence that the likes of Gary Habbermas, Mike Licona, and even William Lane Craig have had to address his content. So, enough of the ad hominems, let's get to the content.

I have a few goals with this post.

1. Show that Than's original disagreement with Paulogia comes from the two of them talking past each other, and I hope to show where this arises in the Bayesian analysis
2. Correct or improve some of Than's notation to make the approach clearer
3. Show where the Than's argument goes awry, and hopefully direct the conversation in a productive direction.

The original problem

It starts with Paulogia's tweet:

Than replies

"This sounds clever—until you think about it for more than five seconds, because in reality, it reflects a deep misunderstanding of both the methodology and the epistemology behind historical arguments for the resurrection of Jesus."

and later

His one-liner only works if he collapses two distinct things into one. But the Historical Reportage Model (HRM) and the Maximal Data Case are two separate stages of reasoning. They are not interchangeable, and neither functions like the other.

summarized as

So, we separate the historical investigation into two stages:

1. What kind of document were the Gospel authors trying to write? (HRM)
2. Given that, what actually happened? (Max Data Case)

Than's setup

Than defines his data as,

The Maximal Data Case looks at historically accessible facts—such as (but not limited to):

• The crucifixion of Jesus under Pontius Pilate,
• The early proclamation of the resurrection in Jerusalem,
• The empty tomb (as independently attested across traditions),
• The poly-modal,  post-mortem appearances to individuals and groups,
• The conversions of skeptics like James and Paul,
• And the rise of a resurrection-centric movement that exploded across hostile cultural environments…

In other words, given these data points, the question becomes: Which hypothesis best accounts for them? And this is where a formal structure is not just helpful, but necessary.

In formal terms, we are evaluating a likelihood ratio

$$\frac{P(E|H_{\text{Res}}+k)}{P(E|H_{\text{Alt}}+k)}$$ Where:

• $E$ = the body of historical evidence
• $H_{\text{Res}}$ = the resurrection hypothesis
• $H_{\text{Alt}}$ = any competing hypothesis (e.g., hallucination theory, theft, legend)
• $k$ = relevant background knowledge, including the HRM (i.e., that the Gospels are good-faith historical reportage)

Where he notes "HRM is part of the background knowledge (k), not the evidence."

Side quest ad hominem

Than continues

Paulogia’s rhetorical move only works if he collapses two distinct stages of reasoning into one—and then flattens them into “because the Bible says so.” But why does this conflation happen so often?

and

If I am being less charitable, it seems to be because if the Historical Reportage Model (HRM) is granted, the resurrection becomes too evidentially powerful to dismiss without shifting the standards. And that’s a problem for the skeptic.

[...]

And here’s the underlying tension: if you’re already committed to the Humean idea that miracle claims are so improbable that no amount of testimony could ever justify belief, then the Maximal Data Case becomes threatening. Because on explanatory grounds alone, the resurrection might actually come out ahead.

finally,

To avoid facing that dilemma, many skeptics opt to short-circuit the conversation entirely.

What's the real problem?

I really dislike the claim that someone is just performing a "rhetorical move" to "avoid facing" an uncomfortable conclusion -- this seems to invoke mind-reading that I am not confident exists. I've heard it said that it is far too easy to ascribe good reasoning to your side and psychological motives to your opponent, and that is what seems to be happening here. Why would Paulogia state that both HRM and Max Data are equivalent to "for the Bible tells me so"? This is the case even while Than insists that HRM does not imply Biblical inerrancy, taking the stance:

A critic could accept HRM and still say, “Yes, Luke wrote what he believed was accurate—but his sources were wrong.” That’s a fair counter-hypothesis. What’s not fair is pretending that HRM means “Jesus rose because the Gospels say so.” That’s either a category error—or a straw man.

The problem is the following. If you accept the Historical Reportage Model (HRM) (" [the Gospel authors] sought to record the deeds and teachings of Jesus in good faith, based on sources they considered reliable (including eyewitnesses and early oral tradition), and they did not see themselves as having literary license to invent or reshape historical events for purely theological, symbolic, or moral purposes") then you accept things like the authors were eyewitnesses and honestly claimed to have eaten fish and touched the wounds of Jesus after he was crucified and buried for three days. No skeptic accepts this, and the only reason to accept the fish and the wounds story is in fact "for the Bible tells me so" -- the Gospels (and sometimes only one Gospel) is the only source for these stories. The Max Data case, as described in mathematical detail by Than, assumes HRM at every point so it too inherits the "for the Bible tells me so"

All of the math that Than provides doesn't change this fact, but I think we can make it more clear by doing the analysis again, correcting some things along the way, see where Than's analysis fits into the correction and see where that lands us.

An improved solution

Before we embark on the improved solution, we have to state what the problem is. Essentially we are evaluating the claim of the Resurrection, and want to know simply,

$$P(R|\text{data})$$ where $R$ represents the model/hypothesis of the Resurrection. In order to accomplish this we need to:

1. specify our alternative models
2. be specific about what our data is

In both of these steps Than drops the ball.

Alternative models

It is annoying that Christian apologist always (note: I'd love to see an exception) pull out the least charitably alternative explanations of the Biblical data, and Than is no exception. He comments on hallucination, theft, and legend only. At least he doesn't bother critiquing the swoon theory, which no modern skeptic has ever suggested. What he doesn't do is look at specific alternatives and their explanatory value on the Biblical data, such as James Fodor's RHBS model, Paulogia's Minimal Witnesses model, and Kamil Gregor's Pareidolia model. I find this problematic, because it is easy to argue against the hallucination if you assume that the Biblical texts are mostly reliable and they say that 500 people saw Jesus after 3 days, but this ends up being a strawman. So our problem now becomes,

$$\begin{array}{rl}P(R|\text{data})& =...\\ P(\text{RHBS}|\text{data})& =...\\ P(\text{Minimum-Witnesses}|\text{data})& =...\\ P(\text{Pareidolia}|\text{data})& =...\\ ⋮& \end{array}$$ for all of the models that we want to explore. As a practical matter, when you have more than two models (and even many times with only two models) the full fractional form of the Bayes theorem gets hard to fit easily on the page. The denominator especially can get very long, and obscure the calculation. As such I will use the approach that I describe in my book Statistical Inference for Everyone where I write out the numerators only (and use the ~ symbol instead of =), sum those numerators to a separate term, and then divide by the sum as an extra step. Examples of this can be found here and here. This allows us to seamlessly include as many models as we wish.

Having just said that, also for convenience, I will follow Than's approach and just lump all the alternatives into one, which I'll call $A$, but keep in mind that to do this properly at the end we need to break that out into some of the specific cases.

The data

The next problem Than has is with the data. He presents things like the "historically accessible facts" above, but that is not the data. The data is "we have texts that have stories about..." those "historically accessible facts". For example, the empty tomb is not something that needs to be explained (although the RHBS model does do that), what we have to explain is "we have texts that have stories about...an empty tomb". The Minimal Witnesses model, for example, states that the entire empty tomb narrative -- which stems from one source only -- is easily explained as a fictitious addition to explain certain counter apologetics at the time. The character of Joseph of Arimathea in whose tomb Jesus is supposedly buried has all the hallmarks of a made up character to satisfy certain plot points in the story. Either way, the data could be explained with Than's HRM model but can also be explained with more literary models.

A side note about notation and mistakes

When Than writes down his odds form for the posterior, he writes:

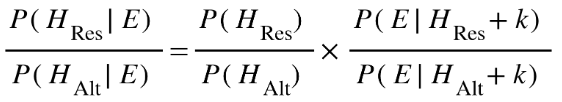
First, one would never use the "+" operator to denote extra information. In logic, "+" is attributed to the "or" operation, not the "and" operation which Than wants. One can use "$\cdot$", "," or ";" instead. Also, this "background information" denoted by $k$ should be in all of the terms, not just in the likelihood term. This mistake makes Than think his conclusions are more general than they are. A proper rewriting of this, using Than's notation, is

$$\frac{P(H_{\text{Res}}|E,k)}{P(H_{\text{Alt}}|E,k)}=\frac{P(H_{\text{Res}}|k)}{P(H_{\text{Alt}}|k)}\times \frac{P(E|H_{\text{Res}},k)}{P(E|H_{\text{Alt}},k)}$$ where $k$ includes the Historical Reportage Model (HRM). To make this more explicit, and to reduce the number of symbols, and further to avoid some issues with the odds form, I prefer to write this same equation as,

$$\begin{array}{rl}P(R|\text{data},\text{HRM})& \sim P(\text{data}|R,\text{HRM})\cdot P(R|\text{HRM})\\ P(A|\text{data},\text{HRM})& \sim P(\text{data}|A,\text{HRM})\cdot P(A|\text{HRM})\end{array}$$

Calculating the posterior - a marginalization step

It is my contention that Paulogia (and myself) care about $P(R|\text{data})$ and we don't care much about $P(R|\text{data},\text{HRM})$, while Than cares more about the latter than the former -- or at least only addresses the latter not the former. As such, Than interprets Paulogia's dismissal of HRM and the Max Data as "for the Bible tells me so" as a rhetorical move, when in fact they are each talking about different mathematical terms. In order to handle this mathematically we need to relate these two terms, which we can do with a process of marginalization (see page 105 in Loredo's excellent From Laplace to Supernova paper). All this is, is a process of breaking up a single probability term, i.e. $P(H)$, into a sum of terms conditional on a variable and multiplied by the prior of that variable,

$$P(H)=P(H|A)P(A)+P(H|\neg A)P(\neg A)$$ Applying this to the case at hand we have,

$$\begin{array}{rl}P(R|\text{data})& \sim P(\text{data}|R)\cdot P(R)\\ & \sim \left[P(\text{data}|R,\text{HRM})\cdot P(\text{HRM}|R)+P(\text{data}|R,\neg \text{HRM})\cdot P(\neg \text{HRM}|R)\right]\cdot P(R)\\ P(A|\text{data})& \sim P(\text{data}|A)\cdot P(A)\\ & \sim \left[P(\text{data}|A,\text{HRM})\cdot P(\text{HRM}|A)+P(\text{data}|A,\neg \text{HRM})\cdot P(\neg \text{HRM}|A)\right]\cdot P(A)\end{array}$$

I don't see why knowing either $R$ or $A$ should effect the probability of HRM, so this simplifies a bit to:

$$\begin{array}{rl}P(R|\text{data})& \sim \left[P(\text{data}|R,\text{HRM})\cdot P(\text{HRM})+P(\text{data}|R,\neg \text{HRM})\cdot P(\neg \text{HRM})\right]\cdot P(R)\\ P(A|\text{data})& \sim \left[P(\text{data}|A,\text{HRM})\cdot P(\text{HRM})+P(\text{data}|A,\neg \text{HRM})\cdot P(\neg \text{HRM})\right]\cdot P(A)\end{array}$$

Reproducing Than's numbers

In the article, Than assigns the following prior probabilities

• $P(R)=10^{-6}=0.000001$
• $P(A)=1-10^{-6}=0.999999$

and the following likelihood values given independent evidence/data which he calls $E_1$ (e.g. crucifixion), $E_2$ (e.g. Multi-Modal Post-Mortem Appearances), and $E_3$ (Conversion of Skeptics):

• $P(E_1|R,\text{HRM})=0.5$, $P(E_2|R,\text{HRM})=0.9$, $P(E_3|R,\text{HRM})=0.8$
• $P(E_1|A,\text{HRM})=0.5$, $P(E_2|A,\text{HRM})=0.0001$, $P(E_3|A,\text{HRM})=0.001$

His analysis at all points assumes HRM is true, so he implicitly assigns,

• $P(\text{HRM})\approx 1$
• $P(\neg \text{HRM})\approx 0$

Plugging these into the equations above,

$$\begin{array}{rl}P(R|\text{data})& \sim \left[P(\text{data}|R,\text{HRM})\cdot P(\text{HRM})+P(\text{data}|R,\neg \text{HRM})\cdot P(\neg \text{HRM})\right]\cdot P(R)\\ & \sim \left[0.5\cdot 0.9\cdot 0.8\cdot 1+P(\text{data}|R,\neg \text{HRM})\cdot 0\right]\cdot 0.000001\\ P(A|\text{data})& \sim \left[P(\text{data}|A,\text{HRM})\cdot P(\text{HRM})+P(\text{data}|A,\neg \text{HRM})\cdot P(\neg \text{HRM})\right]\cdot P(A)\\ & \sim \left[0.5\cdot 0.0001\cdot 0.001\cdot 1+P(\text{data}|A,\neg \text{HRM})\cdot 0\right]\cdot 0.999999\end{array}$$

which leads to:

$$\begin{array}{rl}P(R|\text{data})& \sim 3.6\cdot 10^{-7}\\ P(A|\text{data})& \sim 5\cdot 10^{-8}\\ T& =3.6\times 10^{-7}+5\cdot 10^{-8}=4.1\cdot 10^{-7}\end{array}$$ and finally

$$\begin{array}{rl}P(R|\text{data})& \sim 3.6\cdot 10^{-7}/T=0.878\\ P(A|\text{data})& \sim 5\cdot 10^{-8}/T=0.122\end{array}$$ which agrees with Than.

Where now?

The big issue is that no skeptic thinks that $P(\text{HRM})$ is likely, instead it would be $P(\text{HRM})\ll P(\neg \text{HRM})$. Where $\neg \text{HRM}$ includes mixtures, where the texts include some historical elements, some embellishments, some fabrications, etc... What does the calculation look like now?

We start with this, $$\begin{array}{rl}P(R|\text{data})& \sim \left[P(\text{data}|R,\text{HRM})\cdot P(\text{HRM})+P(\text{data}|R,\neg \text{HRM})\cdot P(\neg \text{HRM})\right]\cdot P(R)\\ P(A|\text{data})& \sim \left[P(\text{data}|A,\text{HRM})\cdot P(\text{HRM})+P(\text{data}|A,\neg \text{HRM})\cdot P(\neg \text{HRM})\right]\cdot P(A)\end{array}$$ and admit that even under the $\neg \text{HRM}$ model, the Resurrection hypothesis fits the data well but so do the alternatives, so we'd have $P(\text{data}|H,\neg \text{HRM})\approx P(\text{data}|A,\neg \text{HRM})$ which we will define as "same". Since $P(\text{HRM})\ll P(\neg \text{HRM})$, the first term nearly drops out, and the calculation becomes, $$\begin{array}{rl}P(R|\text{data})& \sim \left[\text{(high)}\cdot 0+\text{(same)}\cdot 1\right]\cdot P(R)\\ P(A|\text{data})& \sim \left[\text{(low)}\cdot 0+\text{(same)}\cdot 1\right]\cdot P(A)\end{array}$$ So the calculation boils down the priors, and the data has a negligible effect,

$$\begin{array}{rl}P(R|\text{data})& =P(R)\\ P(A|\text{data})& =P(A)\end{array}$$ Why is that? It's because mundane models can explain the "texts contain stories" data and don't need to explain the "texts contain facts" data.

If one wanted to be more precise here, one would need to look at specific models as I said earlier, and actually handle those alternatives and what the data actually contain.

Some random comments about other claims in the article

While I'm here, there are some other random thoughts I had on the article.

• The "facts" as Than lists as being easily explained under the resurrection are incomplete -- the list does not contain things not observed that are hard to explain if the events happened as stated. This includes,
  • no mention of Joseph of Arimathea after the empty tomb story
  • no mention of many of the specific apostles after the tomb story
  • the inconsistent messaging of Jesus (e.g. meet Galilee or Jeruselem?)
  • no search by the Romans for a stolen body -- which would be the way they would have interpreted things
  • no support for ascension other than "for the Bible tells me so", which is a requirement for the rest of the story to make sense
  • I could go on here, but these are things that are easily explained under any of the alternatives but are not explained well if the resurrection actually happened
• All the Humean critique is misplaced. While I don't entirely agree with Hume's wording of the "uniformity of nature" argument, you'd be hard pressed to interpret Hume's argument against testimony (e.g. avoid the greater miracle) as not being a simple application of Bayes Theorem.
• Than's prior of one in a million for the resurrection is ludicrously too large. A very simple estimate, taking the entire known population ever to have lived on the planet (around 20 billion) with at most 1 resurrection puts it below one in twenty billion. Add to that our understanding of biology, of the psychology of extraordinary claims, etc.. will put this well below that.
• Paulogia has stated many times that testimony alone cannot convince him of a miracle. I agree completely. I would also phrase it like, testimony alone cannot convince me that particles can move faster than the speed of light. This is not even a supernatural claim -- so it is more likely than a resurrection -- yet it has the same structure. I am not employing a naturalistic bias, and evidence could convince me, but not all evidence is the same.
• While Than trots out that enough "independent evidence" could support a miracle, a calculation the McGrews like to use, it is seriously flawed. I show here that "one can be supremely confident that all 15 sources are statistically independent, at probability of $p=0.9995$ (which is far higher than many scientific claims in published journals), and still not be able to justify the miracle claim due to the small uncertainty." And I show here that "the effect of claims being shown to be unreliable can make further testimony less reliable, even in a model which has a definitively pro-miracle bias."
• I have dealt with miracles in many places, including a very long discussion on miracles going through claim by claim and a discussion on miracles in the Still Unbelievable podcast. As a side comment, Than referred to a miracle healing in his debate with Matt Dillahunty, which Matt later shows has no documentary support -- making it worse than even all of the miracle claims we looked at in the long discussion on miracles.

What problems are you interested in? How can I help?

• @bblais
• bblais@bryant.edu
• (401) 232-6153
• Bryant University
  1150 Douglas Pike
  Smithfield, RI
  02917 US