Stats 101 Examples with MCMC Part 4

Estimating a central value with a Cauchy Distribution

In #MCMC #Bayesian #math

This is another in the series of "Statistics 101" examples solved with MCMC. Others in the series:

In all of these posts I'm going to use a python library I make for my science-programming class, stored on github, and the emcee library. Install like:

pip install "git+git://github.com/bblais/sci378" --upgrade
pip install emcee

In this example, like another one in the series, there is some true value, we call \(x_o\). The \(N\) data points we have, \(\{x_i\}\), consist of that true value drawn from a particular distribution, in this case the Cauchy distribution:

$$ P(x|\mu,\gamma)= \frac{1}{\pi\gamma}\left(\frac{\gamma^2}{(x-x_o)^2+\gamma^2}\right) $$

This distribution has a number of applications, many of which occur in cases of circular geometry. I was introduced to it with the so-called lighthouse problem and E T Jaynes's excellent Confidence Intervals vs Bayesian Intervals paper.

Although this distribution has a single-peak with a central value, \(x_o\), and looks vaguely Gaussian, it has many mathematical properties which make it much different. For example, it has an undefined mean and variance, and thus doesn't satisfy the conditions for the central limit theorem. As such it is never covered in introductory statistics classes. However, with the computational approach described here, it is no harder to work with the Cauchy than the Normal.

Setting up the problem

In E T Jaynes's example, the data consist simply of two data points: \(\{x_i\} = \{3,5\}\). Remarkably, frequentist methods can't address this problem. The likelihood is set in the same way as previous posts:

def lnlike(data,x_o,γ):
    x=data
    return logcauchypdf(x,x_o,γ)

data=array([3.,5])
model=MCMCModel(data,lnlike,
                x_o=Uniform(-50,50),
                γ=Jeffreys()
                )

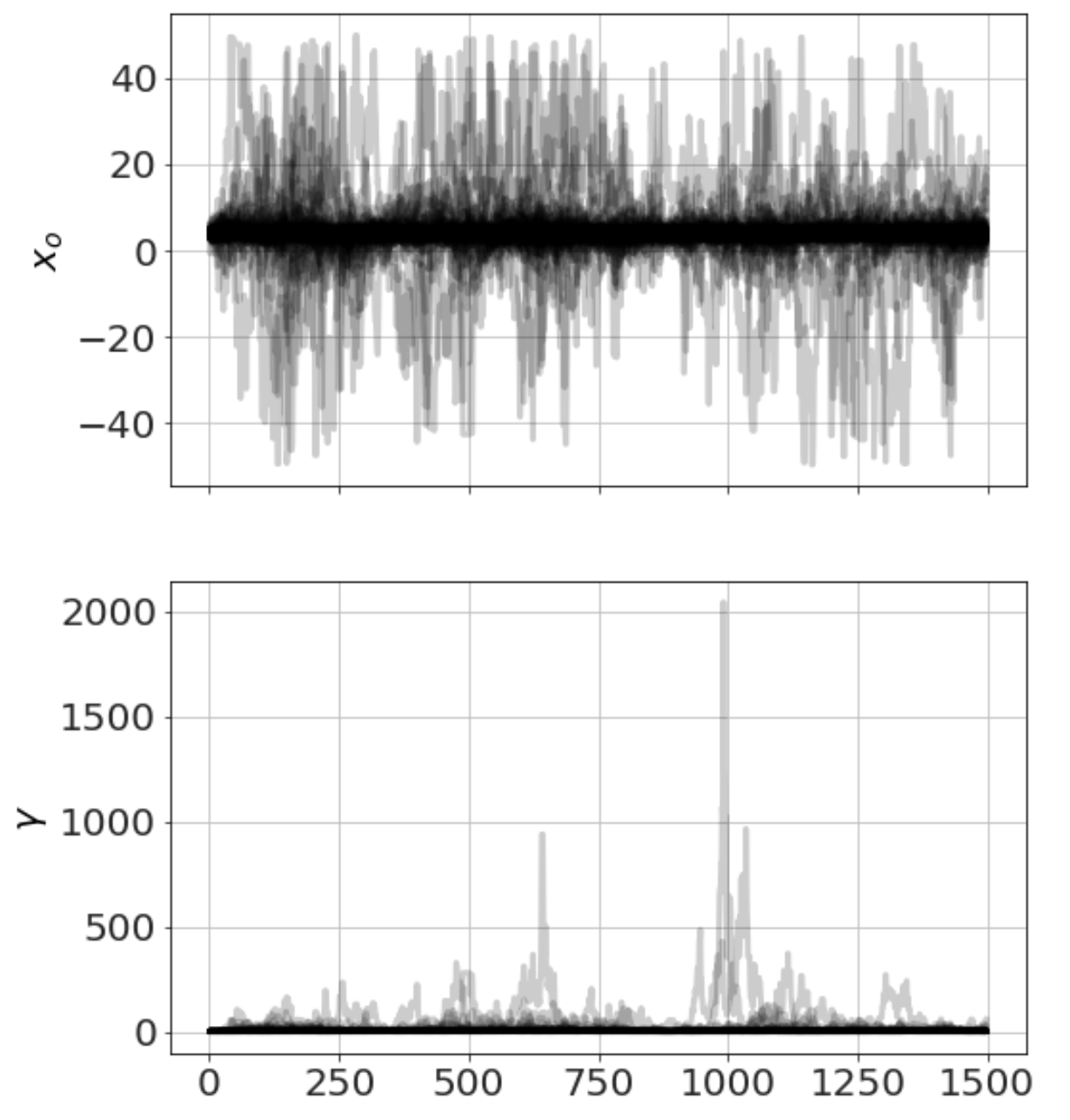
Running MCMC, looking at the results

Now we run MCMC, plot the chains (so we can see it has converged) and look at distributions,

model.run_mcmc(1500,repeat=3)
model.plot_chains()

Sampling Prior...
Done.
0.43 s
Running MCMC 1/3...
Done.
3.74 s
Running MCMC 2/3...
Done.
3.61 s
Running MCMC 3/3...
Done.
3.66 s


model.plot_distributions()

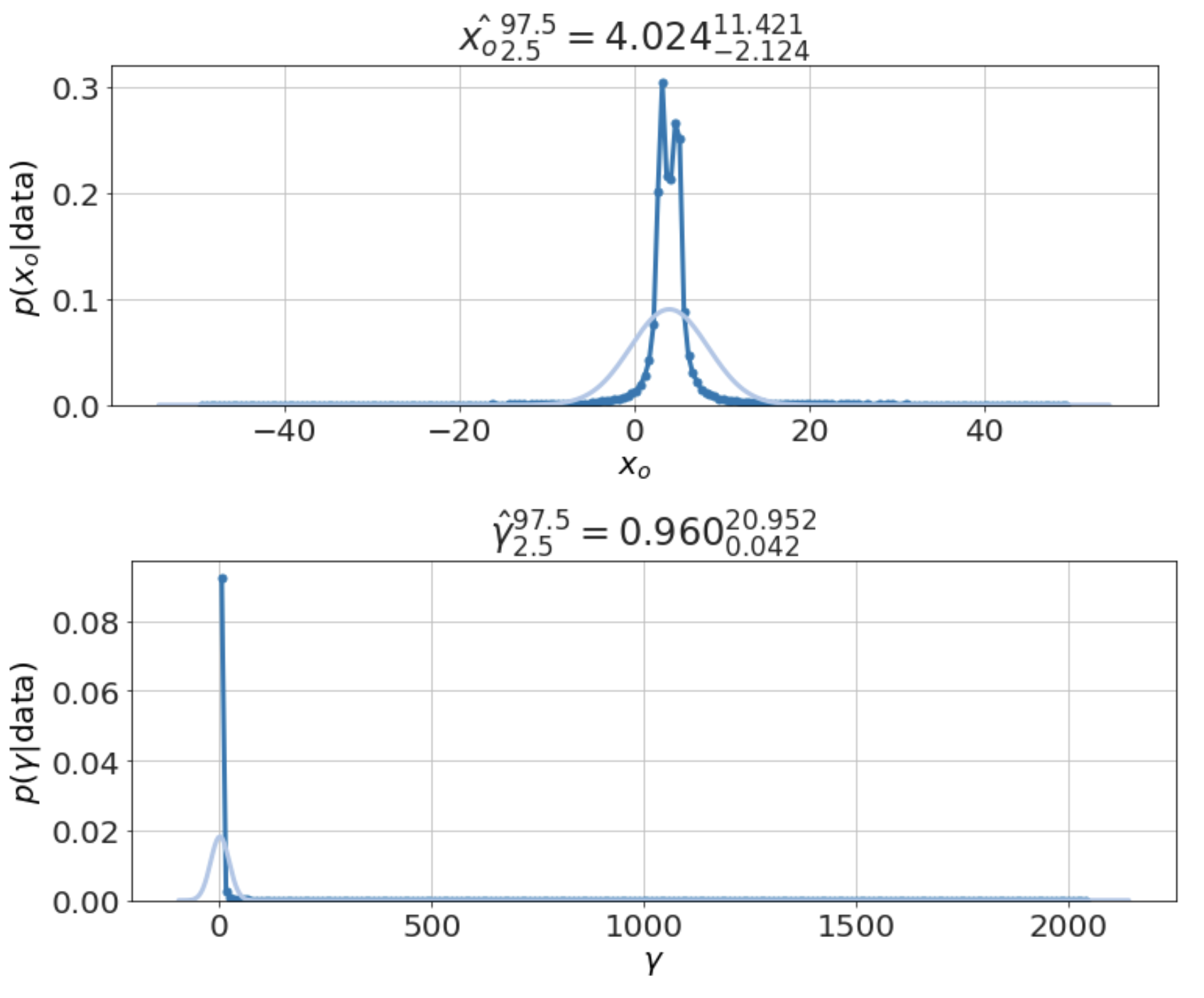
Comparing to intution and conclusions

Although the Cauchy has no defined mean value, one can show that the median of the data is a best estimate for the central value, \(x_o\) -- although that doesn't give the uncertainties. Thus, the estimate we find above, \(x_o \sim 4\), matches what we intuit to be the correct answer.

The point here, however, is that the same Bayesian methods for finding the best estimates and the uncertainties works for this case like all the others -- with very little extra work -- whereas traditional methods fail. It is telling that statistics textbooks uniformly ignore this entire distribution as far as I can tell just to avoid the problems with it. The Bayesian approach, in contrast, provides a uniform procedure to address all such problems and that procedure consistently produces useful results.